ecshop跨站漏洞详情及修补网站漏洞

ecshop目前最新版本为4.0，是国内开源的一套商城系统，很多外贸公司，以及电商平台都在使用，正因为使用的人数较多，很多攻击者都在挖掘该网站的漏洞，就在最近ecshop被爆出高危漏洞，该漏洞利用跨站伪造函数，来对网站数据库进行攻击。

ecshop 漏洞详情

该网站漏洞发生的根本原因是根目录下的user.php文件，在第315-365行里的代码里，该代码主要是处理用户注册，用户登录的一些功能请求处理，与数据库进行通信查询用户的账号密码是否正确，以及写入数据库中用户的注册资料等信息。我们使用一台windows2008服务器来搭建下ecshop系统的环境，我们使用IIS7.5+mysql数据库，php的版本为5.3，在官方下载最新版。

我们来看下发生问题的user.php代码，如下图：

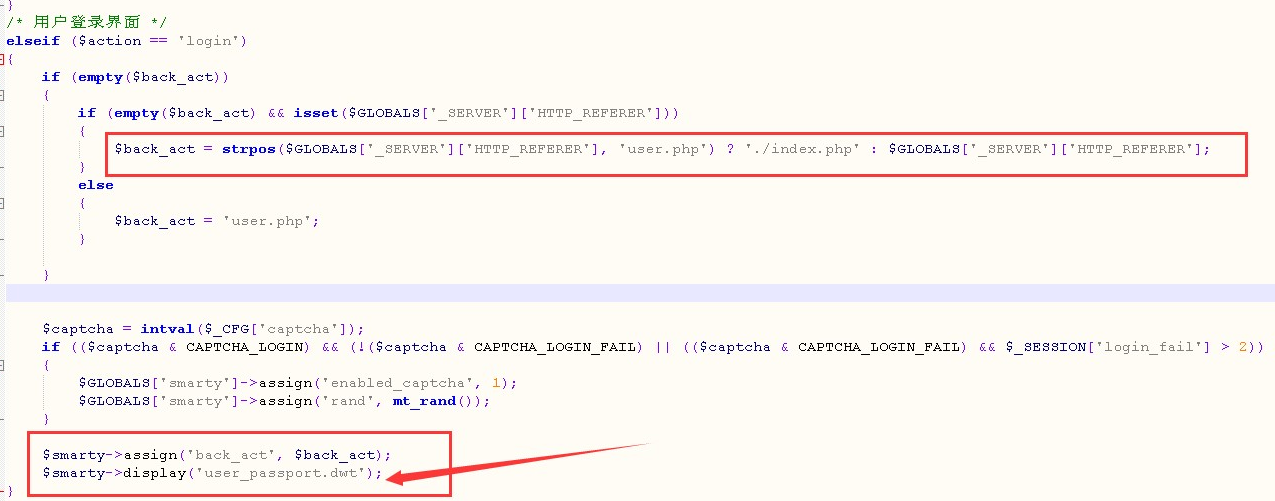
从上面的代码可以看出，用户在登录的时候会先将变量值action传入到login进行赋值变成登录的主要代码，当登录请求的时候，系统会将referer里的值传递给back_act这个参数里，导致网站漏洞发生，由于传入的参数可以传递给assign的函数中去，导致模板注册给改变了变量，可以插入跨站脚本攻击代码进去，直接插入到html文件里。

本身ecshop网站，当初设计的时候就有安全拦截系统，对一些非法的参数，攻击代码进行了强制的转换与拦截，有一些安全的拦截规则，我们可以从includes目录下的safety.php文件可以看出来，如下图：

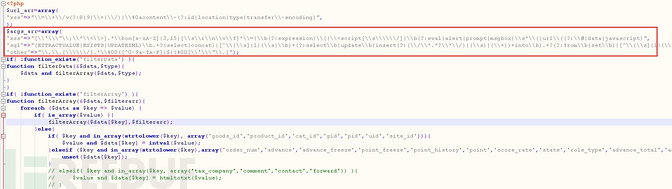
网站系统的拦截规则写的非常简单，只是过滤了常用的html标签以及eval一句话代码的特征，一些敏感的特殊字符，像《》*%#都拦截掉了。但是ecshop官方疏忽了JS跨站弹窗的一个函数，confirm可以直接插入代码进行使用，漏洞的使用就是绕过ecshop安全拦截规则，把攻击代码直接写入到html里。我们可以使用html的编码方式进行绕过，构造如下的代码：

GET /ECShop4.0/user.php

HTTP/1.1

Referer:" /><a href=j&#97v&#97:&#97lert

('Cyc1e_test')><imgsrc="xxxxx

User-Agent:Mozilla/5.0 (Windows NT 6.1; WOW64) AppleWebKit/537.21

(KHTML, like Gecko)Chrome/41.0.2228.0

Safari/537.21Cookie:ECS_ID=17b608d2a679cf2c7e8611581478e6929dbfb34b;ECS

[visit_times]=2Connection:keep-aliveAccept: */*Accept-

Encoding:gzip,deflateHost:

利用get的提交方式将我们构造的恶意代码写入到数据包中，提交到网站里。这样直接绕过了ecshop的安全检测，该漏洞的使用需要用户点击图片才可以使漏洞正常使用。

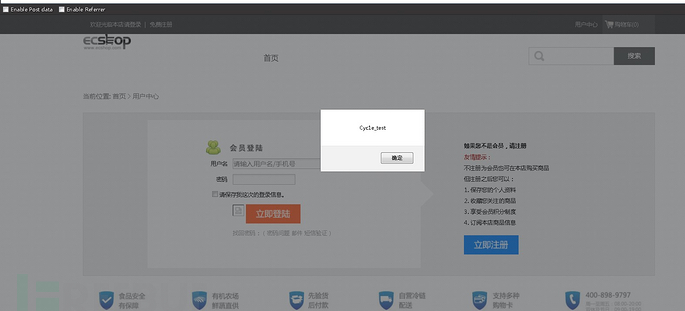
关于ecshop网站漏洞的修复建议：

对ecshop safety.php文件进行安全过滤，对#97以及href，，进行强制的拦截，html实体编码也进行拦截，如果对代码不是太懂的话，也可以对模板文件进行安全权限限制，ecshop官方目前没有对此跨站漏洞进行漏洞修复与升级补丁，建议使用4.0版本的网站，删除user.php注册功能，如果自己懂程序，那就可以自己针对代码的漏洞进行ecshop漏洞修复，不懂的话，可以找专业的网站安全公司来修复ecshop漏洞，国内像SINE安全、绿盟安全、启明星辰都是比较专业的安全公司，很多攻击者之所以能植入木马病毒，就是抓住了ecshop网站代码上的漏洞。