{转}用ADMM求解大型机器学习问题

[本文链接：http://www.cnblogs.com/breezedeus/p/3496819.html]

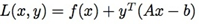从等式约束的最小化问题说起：                                                                                          上面问题的拉格朗日表达式为：                                                也就是前面的最小化问题可以写为：                                               minxmaxyL(x,y) 。 它对应的对偶问题为：                                              maxyminxL(x,y) 。 下面是用来求解此对偶问题的对偶上升迭代方法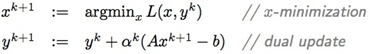：                                      这个方法在满足一些比较强的假设下可以证明收敛。

为了弱化对偶上升方法的强假设性，一些研究者在上世纪60年代提出使用扩展拉格朗日表达式（augmented Lagrangian）代替原来的拉格朗日表达式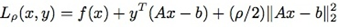：                                    其中ρ>0。对应上面的对偶上升方法，得到下面的乘子法（method of multipliers）：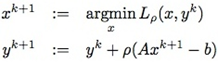                                                     

注意，乘子法里把第二个式子里的αk改成了扩展拉格朗日表达式中引入的ρ。这不是一个随意行为，而是有理论依据的。利用L(x,y)可以导出上面最小化问题对应的原始和对偶可行性条件分别为（∂L∂y=0，∂L∂x=0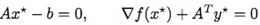）：                                                 既然xk+1 最小化 Lρ(x,yk)，有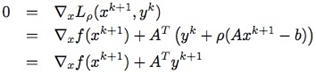：                                          上面最后一个等式就是利用了yk+1=yk+ρ(Axk+1−b)。从上面可知，这种yk+1的取法使得(xk+1,yk+1)满足对偶可行条件∂L∂x=0。而原始可行条件在迭代过程中逐渐成立。

乘子法弱化了对偶上升法的收敛条件，但由于在x-minimization步引入了二次项而导致无法把x分开进行求解（详见[1])。而接下来要讲的最小化Lρ(xk+1,z,yk)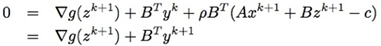：                                         其中用到了z对应的对偶可行性式子：                                                    ∂L∂z=∇g(z)+BTy=0

定义新变量u=1ρy，那么(3.2-3.4)中的迭代可以变为以下形式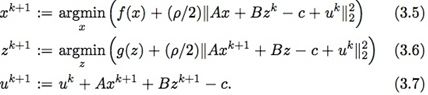：                             在真正求解时通常会使用所谓的over-relaxation方法，也即在z和u中使用下面的表达式代替其中的Axk+1：                                          αkAxk+1−(1−αk)(Bzk−c)， 其中αk为relaxation因子。有实验表明αk∈[1.5,1.8]可以改进收敛性([2])。

下面让我们看看ADMM怎么被用来求解大型的机器学习模型。所谓的大型，要不就是样本数太多，或者样本的维数太高。下面我们只考虑第一种情况，关于第二种情况感兴趣的读者可以参见最后的参考文献[1, 2]。样本数太多无法一次全部导入内存，常见的处理方式是使用分布式系统，把样本分块，使得每块样本能导入到一台机器的内存中。当然，我们要的是一个最终模型，它的训练过程利用了所有的样本数据。常见的机器学习模型如下：                                     minimize x∑Jj=1fj(x)+g(x)， 其中x为模型参数，fj(x)对应第j个样本的损失函数，而g(x)为惩罚系数，如g(x)=||x||1。

假设把J个样本分成N份，每份可以导入内存。此时我们把上面的问题重写为下面的形式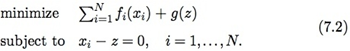：                                               除了把目标函数分成N块，还额外加了N个等式约束，使得利用每块样本计算出来的模型参数xi都相等。那么，ADMM中的求解步骤(3.2)-(3.4)变为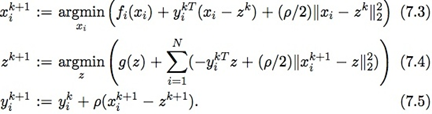：                                例如求解L1惩罚的LR模型，其迭代步骤如下（u=1ρy，g(z)=λ||z||1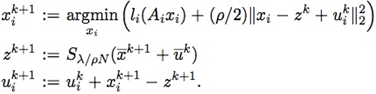）：                                       其中x¯≐1N∑Nixi，y¯的定义类似。

在分布式情况下，为了计算方便通常会把u的更新步骤挪在最前面，这样u和x的更新可以放在一块：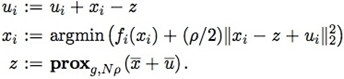                                       

ADMM的框架确实很牛逼，把一个大问题分成可分布式同时求解的多个小问题。理论上，ADMM的框架可以解决大部分实际中的大尺度问题。我自己全部实现了一遍这个框架，主要用于求解LR问题，下面说说我碰到的一些问题： 1. 收敛不够快，往往需要迭代几十步。整体速度主要依赖于xi更新时所使用的优化方法，个人建议使用liblinear里算法，但是不能直接拿来就用，需要做一些调整。 2. 停止准则和ρ的选取：停止准则主要考量的是xi和z之间的差异和它们本身的变动情况，但这些值又受ρ的取值的影响。它们之间如何权衡并无定法。个人建议使用模型在测试集上的效果来确定是否停止迭代。 3. 不适合MapReduce框架实现：需要保证对数据的分割自始至终都一致；用MPI实现的话相对于其他算法又未必有什么优势（如L-BFGS、OwLQN等）。 4. relaxation步骤要谨慎：α的取值依赖于具体的问题，很多时候的确可以加快收敛速度，但对有些问题甚至可能带来不收敛的后果。用的时候不论是用x -> z -> u的更新步骤，还是用u -> x -> z的更新步骤，在u步使用的x_hat要和在z步使用的相同（使用旧的z），而不是使用z步刚更新的z重算。 5. warm start 和子问题求解逐渐精确的策略可以降低xi更新时的耗时，但也使得算法更加复杂，需要设定的参数也增加了。

[References] [1] S. Boyd. Alternating Direction Method of Multipliers (Slides).
[2] S. Boyd et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers, 2010