hiho42 : 骨牌覆盖问题·二

描述

上一周我们研究了2xN的骨牌问题，这一周我们不妨加大一下难度，研究一下3xN的骨牌问题？
所以我们的题目是：对于3xN的棋盘，使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢？
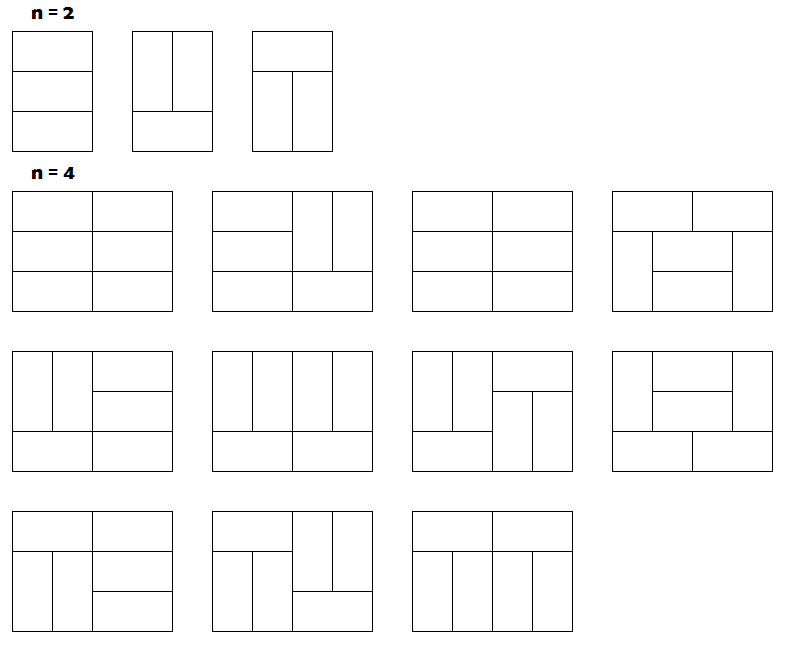
首先我们可以肯定，奇数长度一定是没有办法覆盖的；对于偶数长度，比如2，4，我们有下面几种覆盖方式：

提示：3xN骨牌覆盖

输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 12357

样例输入

62247088

样例输出

4037

提示：3xN骨牌覆盖

在2xN的骨牌覆盖问题中，我们有递推式子 (0,1)xM^n=(f[n-1],f[n])。
我们考虑能否在3xN的情况下找到同样的式子。
但在实际的推导过程可以发现，对于3xN的覆盖，对应的f数值公式比2xN复杂太多。我们需要换个角度来思考推导公式。

在我们放置骨牌的过程中，一定是放好一行之后再放置下一行。根据摆放的方式，可能会产生很多种不同的形状，而这些形状之间是否具有某些递推关系呢？
如果他们存在一定的递推关系，则我们可以根据第i行的方案数来推导第i+1行的方案数。这样一行一行推导，直到第N行时不就得到了我们要求的方案数了么？
那么来研究一下是否存在这样的推导公式吧

假设我们已经放好了一些骨牌，对于当前最后一列(第i列)骨牌，可能有8种情况：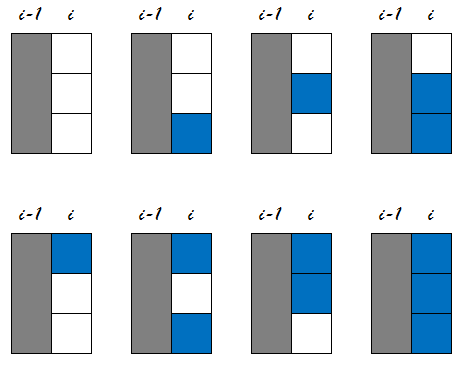

对于上面这8种状态，我们用数字来标记它们。以有放置骨牌的格子为1，未放置为0，转化为2进制数
以最下面一行作为1，则有：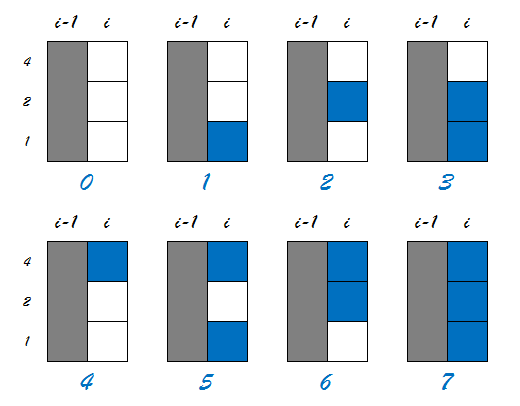

接下来考虑如何放置骨牌，我们先将棋盘旋转一下。假设我们正在放置第i行的骨牌，那么会有下面3种方式：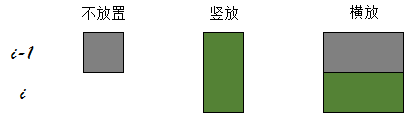

灰色表示已经有的骨牌，绿色表示新放置的骨牌。
每一种放置方法解释如下，假设当第i行的状态为x，第i-1行的状态为y：

• 第i行不放置，则前一行必须有放置的骨牌。x对应二进制位为0，y对应二进制位为1。
• 第i行竖放骨牌，则前一行必须为空。x对应二进制位为1，y对应二进制位为0。
• 第i行横向骨牌，则前一行必须两个位置均有骨牌，否则会产生空位。x对应二进制位为1，y对应二进制位为1。

举个例子：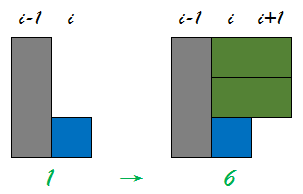

对于第i行状态1，我们在第i+1行竖放两块骨牌之后便能到达状态6。
但是在这之中需要注意会出现下面这种情况：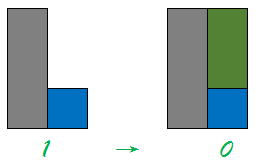

这种情况看似是从状态1变成了状态0，其实是不对的。它不满足我们约定的放置方法，本质是第i行的状态1变成了第i行的状态7，而实际上我们应该放置的是第i+1行。
所以在枚举递推关系的时候一定要注意。
通过枚举8种状态到8种状态的转移，我们可以得到一个8x8的矩阵M（空白的地方均为0）：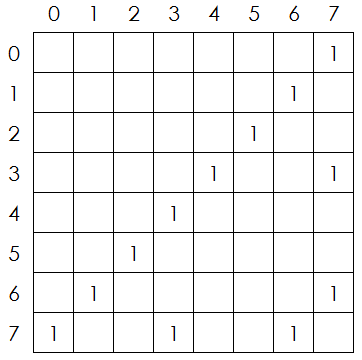

m[i][j]表示从状态i变成状态j的方案数。

现在我们有了M矩阵，接下来考虑边界情况。
在2xN的骨牌覆盖中，有(0, 1)作为初始向量A，那么在3xN中初始向量A是如何呢？
让我们先想想A向量所代表的含义。M矩阵表示状态到状态的转移，则A向量所表示的应该就是第0行各状态的方案数。
同理，对于A * M^n所求出的结果则应该表示为第n行各种状态的方案数。
那么A向量应该是多少呢？很显然，第0行在我们递推的过程中必须看作状态7才合理。故A向量表示为：
{0, 0, 0, 0, 0, 0, 0, 1}
而对于我们寻求的答案，自然也是第n行放置为状态7的方案数了。

 

 

 

#include <iostream>

using namespace std;

typedef long long ll;

const int M = 12357;
struct Matrix
{
	int m[8][8];
	Matrix()
	{

		for(int i=0; i<8; i++)
		{
			for (int j=0; j<8; j++)
			{
				m[i][j]=0;
			}
		}
		for(int i=0; i<8; i++)
		{
			m[i][7-i]=1;
		}
		m[3][7]=1;
		m[7][3]=1;
		m[6][7]=1;
		m[7][6]=1;
	}
	Matrix operator*(Matrix& a)
	{
		Matrix res;

		for (int i=0; i<8; i++)
		{
			for (int j=0; j<8; j++)
			{
				res.m[i][j]=0;
				for (int k=0; k<8; k++)
				{
					res.m[i][j]=(res.m[i][j] + (ll)m[i][k]*a.m[k][j])%M;
				}
			}
		}
		return res;
	}
};

Matrix pow(Matrix m, int n)
{
	Matrix res;
	if(1==n)
		return m;
	res = pow(m, n/2);
	if(n%2==1)
		res = res*res*m;
	else
		res = res*res;
	return res;
}

int main()
{
	int N;
	cin>>N;

	Matrix mat;

	mat = pow(mat, N);

	cout<<mat.m[7][7];

	return 0;
}