3D数学基础：3D游戏动画中欧拉角与万向锁的理解

首先来看一下什么是欧拉角（Euler angles）？
构件在三维空间中的有限转动，可依次用三个相对转角表示，即进动角、章动角和自旋角，这三个转角统称为欧拉角。——引自百度百科
莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于任何一个参考系，一个刚体的取向，是依照顺序，从这参考系，做三个欧拉角的旋转而设定的。所以，刚体的取向可以用三个基本旋转矩阵来决定。换句话说，任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的。——引自wikipedia

好了，引完了，我来说一下我的理解吧，欧拉角是对旋转的一种刻画方式，就像其他刻画方式一样如旋转矩阵，四元数。欧拉角对应的旋转矩阵可以看作是三个绕轴旋转的旋转矩阵的复合。
问题来了，三个绕轴旋转的旋转矩阵绕的是什么坐标系下的轴？
对于坐标系E下的欧拉角(α，β，r)和以下哪个旋转矩阵是等价的
1.绕坐标系E下的x轴旋转α，绕坐标系E下的y轴旋转β，绕坐标系E下的z轴旋转r，三个矩阵的复合
2.绕坐标系E下的x轴旋转α，绕 坐标系E在绕x轴旋转α后的新系E'下的y轴旋转β，绕 坐标系E'在绕y轴旋转β后的新系E''下的z轴旋转r，三个矩阵的复合
通俗的讲，我们在旋转时，要不要把坐标系一起转动？
事实上两种理解都可以，当然，两种转法并不等价，下面我来解释这个问题，
当我们讲到坐标系E下的欧拉角(α，β，r)时，这句话是有歧义的，我们必须定义旋转顺序，因为旋转顺序会影响旋转结果。
如果假设旋转顺序是先绕x轴再y轴再z轴，x-y-z，那么这个欧拉角对应的旋转矩阵是指上述的2所表示的旋转矩阵。
如果假设旋转顺序是先绕z轴再y轴再x轴，z-y-x，那么这个欧拉角对应的旋转矩阵是指上述的1所表示的旋转矩阵，等等，你肯定会问，这难道不是把2中的先后顺序换一下就行了吗，"绕坐标系E下的z轴旋转r，绕 坐标系E在绕z轴旋转r后的新系E'下的y轴旋转β，绕 坐标系E'在绕y轴旋转β后的新系E''下的x轴旋转α，三个矩阵的复合"难道不是这样吗？是的，当然也是这样。

下面我来证明两种复合方式是相等的，
为了方便证明我先定义一些记号，
记：
绕坐标系E下的x轴旋转α的旋转矩阵为Rx,
绕坐标系E下的y轴旋转β的旋转矩阵为Ry,
绕坐标系E下的z轴旋转r的旋转矩阵为Rz,

绕坐标系E下的z轴旋转r的旋转矩阵为Rr（Rr=Rz），
绕 坐标系E在绕z轴旋转r后的新系E'下的y轴旋转β的旋转矩阵为Rb，
绕 坐标系E'在绕y轴旋转β后的新系E''下的x轴旋转α的旋转矩阵为Ra，

另外，将矩阵R的逆记作R~

求证：Rx*Ry*Rz = Rr*Rb*Ra

证明：
Rr = Rz  定义就是一样的，显然相等

Rb = Rr~*Ry*Rr 要得到绕 坐标系E在绕z轴旋转r后的新系E'下的y轴旋转β的旋转矩阵为Rb，可以先应用Rr~这时可以视作在E下，然后使用E下的旋转Ry绕旧的y轴旋转，在应用Rr转回到E'

Ra = (Rr*Rb)~*Rx*(Rr*Rb) 理由同上

所以 右边=Rr*Rb * Ra
         =Rr*Rb * (Rr*Rb)~*Rx*(Rr*Rb)
         =(Rr*Rb)* (Rr*Rb)~*Rx*(Rr*Rb)
         =Rx*(Rr*Rb)
         =Rx*(Rr*Rr~*Ry*Rr)
         =Rx*Ry*Rz =左边 
#证毕

这与DirectX在文档中对D3DXMatrixRotationYawPitchRoll的描述是一致的

D3DXMATRIX * D3DXMatrixRotationYawPitchRoll(
  D3DXMATRIX *pOut,
  FLOAT Yaw,     //绕y轴的转动角
  FLOAT Pitch,   //绕x轴的转动角
  FLOAT Roll     //绕z轴的转动角
);

The order of transformations is roll first, then pitch, then yaw. Relative to the object's local coordinate axis, this is equivalent to rotation around the z-axis, followed by rotation around the x-axis, followed by rotation around the y-axis.

关于欧拉角讲到这里就差不多了，下面来探讨一个和欧拉角有关的概念万向节死锁。

讲到欧拉角一般都会提到万向节死锁，什么是万向节死锁（Gimbal Lock）呢？
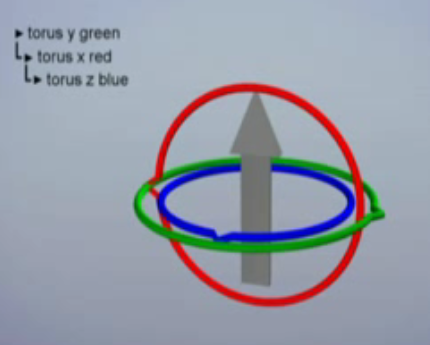
万向节死锁有时又被简称为万向节锁或者万向锁，是指当三个万向节其中两个的轴发生重合时，会失去一个自由度的情形。
下面的视频很好的说明了这一点。

视频: 欧拉旋转

正因万向节死锁的存在，使用欧拉角是无法实现球面平滑插值的，

　　如上图，此时如果下一帧要让箭头指向右侧后方，那么绿色和蓝色对应的旋转角必定要发生突变，因为目前如果想朝着垂直红色圈的方向旋转箭头就像被卡住一样，我想这就是叫它死锁的原因吧。
　　总之万向节死锁会导致位置上连续变化 在数值表示上确是非连续的。给定的两个关键帧之间无法平滑过渡。顺便提一下解决方法，可以使用四元数球面线性插值(Slerp)