POJ2528Mayor's posters 线段树，离散化技巧

• 题意：一个坐标轴从1~1e7，每次覆盖一个区间（li,ri），问最后可见区间有多少个（没有被其他区间挡住的）
• 线段树，按倒序考虑，贴上的地方记为1，每次看（li，ri）这个区间是否全是1，全是1就说明在它后面贴的把它给挡住了，否则该海报可见。
• 然后就愉快的MLE了。。。。
• 再看看数据范围，离散化如下，比如如果海报的左右端点如下
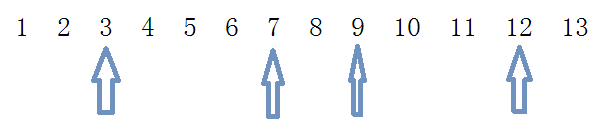
• 那图中橙色的一块的大小其实对结果没有影响，可以把他们都缩为1

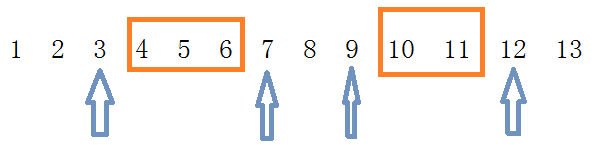
• 最后离散化结果如下图：

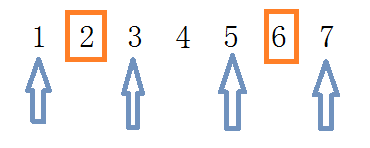
• 代码：

   #include <algorithm>
   #include <iostream>
   #include <cstdio>
   #define nmax 10010
   #define tn t[node]
   #define sl (node<<1)
   #define sr (1+(node<<1))
  
   using namespace std;
   int n;
   int inl[nmax],inr[nmax];
   struct tin{
       int pd,id,num,n2; //0 ->l  1->r
       bool operator < (const tin x) const { return x.num>num; }
   }in[nmax*];
   struct segt { int l,r,v; }t[nmax*];
  
   void build(int node,int l,int r){
       tn.l=l;
       tn.r=r;
       tn.v=;
       if(l==r) return;
       int mid=(l+r)>>;
       build(sl,l,mid);
       build(sr,mid+,r);
   }
  
   int upd(int l,int r,int node,int tv){
       int ta=(tv||tn.v);
       if(tn.l>=l&&tn.r<=r) tn.v=;
       else{
           int mid=(tn.l+tn.r)>>;
           int tl=,tr=;
           if(l<=mid) tl=upd(l,r,sl,tv||tn.v);
           if(r>mid) tr=upd(l,r,sr,tv||tn.v);
           ta=(tl&&tr)||tv;
           tn.v=tn.v||(t[sl].v&&t[sr].v);
       }
       return ta;
   }
  
   int main(){
       int cas;
       cin>>cas;
       while(cas--){
           cin>>n;
           for (int i=; i<n; i++) {
               scanf("%d%d",&in[i].num,&in[i+n].num);
               in[i].pd=;
               in[i+n].pd=;
               in[i].id=in[i+n].id=i;
           }
           sort(in,in+*n);
           //离散化
           int w=;
           in[].n2=(++w);
           for (int i=; i<*n; i++) {
               if(in[i].num==in[i-].num ) {
                   in[i].n2=w;
                   continue;
               }
               in[i].n2=(++w);
               if( in[i].num!=in[i-].num+ ) in[i].n2=(++w);
           }
           //离散化over
           build(,,w);
           for (int i=; i<*n; i++) if(in[i].pd) inr[in[i].id]=in[i].n2; else inl[in[i].id]=in[i].n2;
           int ans=;
           for (int i=n-; i>=; i--) if(upd(inl[i],inr[i],,)==) ans++;
           printf("%d\n",ans);
       }
       return ;
   }