对主定理(Master Theorem)的理解

前言

虽说在学OI的时候学到了非常多的有递归结构的算法或方法，也很清楚他们的复杂度，但更多时候只是能够大概脑补这些方法为什么是这个复杂度，而从未从定理的角度去严格证明他们。因此借着这个机会把主定理整个梳理一遍。

介绍

主定理（Master Theorem)提供了用于分析一类有递归结构算法时间复杂度的方法。这种递归算法通常有这样的结构：

def solve(problem):

    solve_without_recursion()

    for subProblem in problem:

        solve(subProblem)

我们可以用一种表示方式来概括这些结构的算法：对于一个规模为$n$的问题，我们把它分为$a$个子问题，每个子问题规模为$\frac nb$。那么这种方法的复杂度$T(n)$可以表示为：

\[T(n)=a\,T\Big(\frac nb\Big)+f(n)
\]

其中$a\ge 1,b>1$为常数，$\frac{n}{b}$指$\lfloor \frac{n}{b}\rfloor$或$\lceil \frac{n}{b}\rceil$，$f(n)$为创造这些递归或者将这些子问题结果整合的函数。对这个方法我们可以建一个递归树：

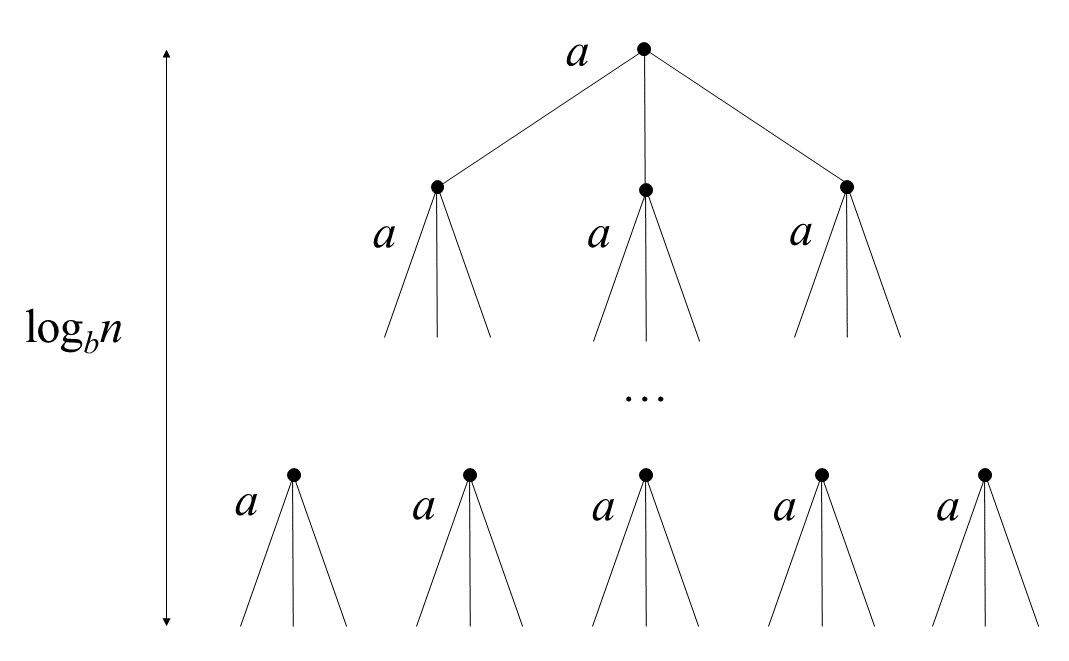
其中树高为$\log_bn$，树的第$i$层有$a^i$个节点，每个节点的问题规模为$\frac{n}{b^i}$。则这棵树有$a^{\log_bn}=n^{\log_ba}$个叶子节点。因此这种方法的复杂度也可以表示为：

\[T(n)=\Theta(n^{\log_ba})+\sum_{i=0}^{\log_bn-1}a^if\Big(\frac{n}{b^i}\Big)
\]

从中我们可以看出，整个方法的复杂度取决于$f(n)$的复杂度。主定理对$f(n)$分了三种情况：

$\exist \varepsilon>0\ s.t.\ f(n)=O(n^{\log_ba-\varepsilon})$。此时$T(n)=\Theta(n^{\log_ba})$。
$f(n)=\Theta(n^{\log_ba})$。此时$T(n)=\Theta(n^{\log_ba}\lg n)$。
$\exist \varepsilon>0\ s.t.\ f(n)=\Omega(n^{\log_ba+\varepsilon})$，且$\exist c<1$，当$n$足够大时，有$a\, f(\frac{n}{b})\le c\, f(n)$。此时$T(n)=\Theta(f(n))$。

$f(n)$含$\log$的情况类似，待补充。

证明

Case 1

令$g(n)=\sum_{i=0}^{\log_bn-1}a^if(\frac{n}{b^i})$，由$f(n)=O(n^{\log_ba-\varepsilon})$，得：

\[g(n)=O\Big(\sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba-\varepsilon}\Big)
\]

之后就是对后面式子的化简：

\[\begin{aligned}
\sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba-\varepsilon} &= n^{\log_ba-\varepsilon}\sum_{i=0}^{\log_bn-1}\Big(\frac{ab^\varepsilon}{b^{\log_ba}}\Big)^i\\
&= n^{\log_ba-\varepsilon}\sum_{i=0}^{\log_bn-1}(b^\varepsilon)^i\\
&= n^{\log_ba-\varepsilon}\Big(\frac{(b^\varepsilon)^{\log_bn}-1}{b^\varepsilon-1}\Big)^i\\
&= n^{\log_ba-\varepsilon}\Big(\frac{n^\varepsilon-1}{b^\varepsilon-1}\Big)^i
\end{aligned}
\]

因此$g(n)=O(\sum_{i=0}^{\log_bn-1}a^i(\frac{n}{b^i})^{\log_ba-\varepsilon})=O(n^{\log_ba})$。所以有：

\[T(n)=\Theta(n^{\log_ba})+O(n^{\log_ba})=\Theta(n^{\log_ba})
\]

Case 2

同Case 1。令$g(n)=\sum_{i=0}^{\log_bn-1}a^if(\frac{n}{b^i})$得：

\[g(n)=\Theta\Big(\sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba}\Big)
\]

继续化简：

\[\begin{aligned}
\sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba} &= n^{\log_ba}\sum_{i=0}^{\log_bn-1}\Big(\frac{a}{b^{\log_ba}}\Big)^i\\
&= n^{\log_ba}\log_bn
\end{aligned}
\]

因此可得$g(n)=n^{\log_ba}\log_bn=n^{\log_ba}\lg n$。所以有：

\[T(n)= \Theta(n^{\log_ba})+\Theta(n^{\log_ba}\lg n)=\Theta(n^{\log_ba}\lg n)
\]

Case 3

还是令$g(n)=\sum_{i=0}^{\log_bn-1}a^if(\frac{n}{b^i})$。但Case 3这里有一个条件：$a\, f(\frac{n}{b})\le c\, f(n)$。我们对这个条件做一下处理：

\[\begin{aligned}
a\, f\Big(\frac{n}{b}\Big) &\le c\, f(n)\\
\Rightarrow f\Big(\frac{n}{b}\Big) &\le \frac{c}{a}f(n)\\
\Rightarrow f\Big(\frac{n}{b^2}\Big) &\le \frac{c}{a}f\Big(\frac nb\Big)\le\Big(\frac{c}{a}\Big)^2f(n)\\
&\vdots\\
f\Big(\frac{n}{b^i}\Big) &\le\Big(\frac{c}{a}\Big)^if(n)\\
\Rightarrow a^i\, f\Big(\frac{n}{b^i}\Big) &\le c^i\, f(n)\\
\end{aligned}
\]

由此我们可以很轻易的向下化简：

\[\begin{aligned}
\sum_{i=0}^{\log_bn-1}a^i\Big(\frac{n}{b^i}\Big)^{\log_ba} &\le \sum_{i=0}^{\log_bn-1}c^i\,f(n)+O(1)\\
&\le f(n)\sum_{i=0}c^i+O(1)\\
&=f(n)\Big(\frac{1}{1-c}\Big)+O(1)\\
&=f(n)
\end{aligned}
\]

得$g(n)=O(f(n))$。又因为$g(n)=\sum_{i=0}^{\log_bn-1}a^if(\frac{n}{b^i})\ge f(n)$，得$g(n)=\Omega(f(n))$。因此$g(n)=\Theta(f(n))$。

所以有：

\[T(n)=\Theta(n^{\log_ba})+\Theta(f(n))=\Theta(f(n))
\]

证毕。

应用

二叉树建树

\[T(n)=2T\Big(\frac{n}{2}\Big)+O(1),\ T(n)=O(n)
\]

此时$\log_ba<1$，满足Case 1。

BFPRT(Median of Medians)

\[T(n)\le T\Big(\frac{n}{5}\Big)+\Big(\frac{7n}{10}\Big)+O(n),\ T(n)=O(n)
\]

此时$\log_ba>1$，即划分之后总规模减小（$1/5+7/10<1$），满足Case 2。

归并排序

\[T(n)=2T\Big(\frac{n}{2}\Big)+O(n),\ T(n)=O(\lg n)
\]

此时$\log_ba=1$，满足Case 3。