目标检测复习之Loss Functions 总结

Loss Functions 总结

损失函数分类: 回归损失函数(Regression loss), 分类损失函数(Classification loss)

Regression loss functions 通常用于模型预测一个连续的值，例如一个人的年龄

Classification loss functions 通常用于模型预测一个离散的值，例如猫狗分类问题

1. L1 loss

Mean Absolute Error(MAE), 也称作L1 loss computes the average of the sum of absolute differences between actual values and predicted values.

• 表达公式:
  
  

• 应用场合: 回归问题，尤其是当目标变量的分布存在异常值时，例如与ping均值相差很大的小值或大值。 它被认为对异常值更稳健。

• Example:

import torch
import torch.nn as nn

input = torch.tensor(
        [[-0.5, -1.5],
        [0.3, -1.3]], requires_grad=True
)

target = torch.tensor(
        [[1.1,  0.5],
        [0.5, -1.5]]
)

mae_loss = nn.L1Loss()
output = mae_loss(input, target)
output.backward()

print('input: ', input)
print('target: ', target)
print('output: ', output)
print('input.grad', input.grad)

• OUTPUT

input:  tensor([[-0.5000, -1.5000],
        		[ 0.3000, -1.3000]], requires_grad=True)
target:  tensor([[ 1.1000,  0.5000],
        		[ 0.5000, -1.5000]])
output:  tensor(1., grad_fn=<L1LossBackward>)  # (按照公式计算)/4
input.grad tensor([[-0.2500, -0.2500],  # (每个值求梯度[符号和target一样])/4
        		  [-0.2500,  0.2500]])

L2 loss

Mean Squared Error(MSE) 也称作L2 loss computes the average of the squared differences between actual values and predicted values

• 表达公式
  
  

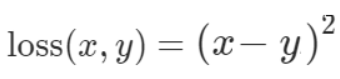
• 应用场合: ping方意味着当预测值离目标更远时在ping方后具有更大的惩罚，预测值离目标更近时在ping方后惩罚更小。 如果分类器错误是 100，则ping方后错误为 10,000。 如果错误是 0.1，则误差为 0.01。 这会惩罚犯大错误的模型并鼓励小错误。相比之下，L1对异常值的鲁棒性更好

• Example

import torch
import torch.nn as nn

input = torch.tensor(
        [[-0.5, -1.5],
        [0.3, -1.3]], requires_grad=True
)

target = torch.tensor(
        [[1.1,  0.5],
        [0.5, -1.5]]
)

mse_loss = nn.MSELoss()
output = mse_loss(input, target)
output.backward()

print('input: ', input)
print('target: ', target)
print('output: ', output)
print('input.grad', input.grad)

• OUTPUT

input:  tensor([[-0.5000, -1.5000],
               [ 0.3000, -1.3000]], requires_grad=True)
target:  tensor([[ 1.1000,  0.5000],
        		[ 0.5000, -1.5000]])
output:  tensor(1.6600, grad_fn=<MseLossBackward>) # (1.6**2 + 2**2 + 0.2**2 +0.2**2)/4 = 1.66
input.grad tensor([[-0.8000, -1.0000],
        		  [-0.1000,  0.1000]])  # (每个值求梯度[符号和target一样])/4 例如：- 2 * (1.1- (-0.5)) / 4 =  -0.8

3. Smoth L1 Loss

• 公式
  
  
• Smoth L1 Loss的优点:
  1. 相比于L1损失函数，可以收验的更快。L1 Loss在0点处导数不唯一，可能影响收验。Smooth L1的解决方法是在0点使用平ping方使得更加平滑
  2. 相比于L2损失函数， 对离群点，异常值不敏感，梯度变化相对更加小，训练时不容易跑飞

4. Cross-Entropy Loss

该损失函数计算提供的一组出现次数或者随机变量的两个概率分布之间的差异。值在0-1之间。

其他的损失函数，例如平(ping)方损失惩罚不正确的预测 负对数似然损失不对预测置信度惩罚，Cross-Entropy惩罚不正确但可信的预测(例如把狗预测成猫并且confidence=0.9)，以及正确但是不可信的预测(例如: 预测对是狗这个类别但是confidence=0.1)

Cross-Entropy有许多种变体，其中最常见的类型是Binary Cross-Entropy(BCE)。BCE Loss主要用于二分类模型即是该模型只有两个类别

• 表达公式

1. softmax表达式:
   
   
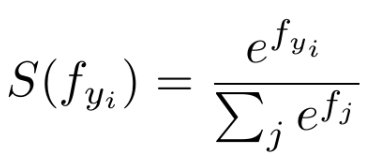
2. Cross-Entropy表达式
   
   
   
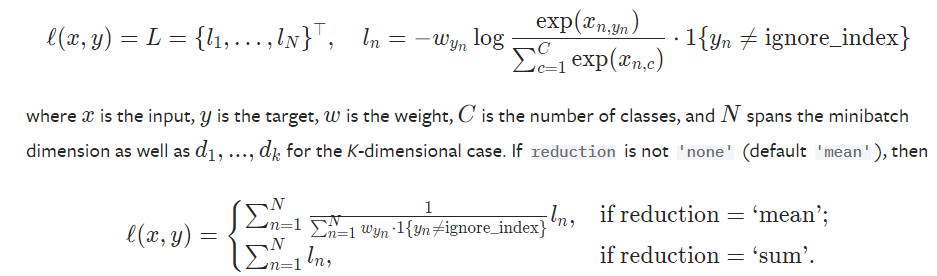
   说明: 在pytorch中值是经过softmax处理过的,并且默认是'mean'处理 可参考: https://stackoverflow.com/questions/49390842/cross-entropy-in-pytorch

• 应用场景: 二分类和多分类

• softmax和Cross-entropy求导证明
  
  参考

1. Softmax求导
   
   
   
   
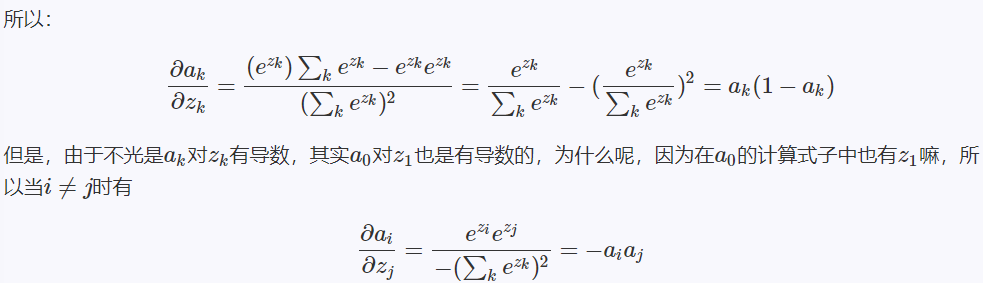
2. Cross-Entropy求导
   
   

• Example1: 上面证明的代码

import torch
import torch.nn as nn

input = torch.tensor(
        [[2., 3., 4.]], requires_grad=True
)

print('softmax:', torch.softmax(input, dim=1))
target = torch.tensor(  # 表示上述位置为1的位置
        [1], dtype=torch.long
)

cross_entropy_loss = nn.CrossEntropyLoss()
output = cross_entropy_loss(input, target)
output.backward()

# print('input: ', input)
# print('target: ', target)
print('output: ', output)

print('input.grad: ', input.grad)

• OUTPUT 求导证明的输出

softmax: tensor([[0.0900, 0.2447, 0.6652]], grad_fn=<SoftmaxBackward>)
output:  tensor(1.4076, grad_fn=<NllLossBackward>)  # 根据公式 -1*ln(0.2447) = 1.4076
input.grad:  tensor([[ 0.0900, -0.7553,  0.6652]])  # 根据求导公式 不是该位置的值为softmax后值(0.0900,0.6652)，该位置值=0.2447-1(-0.7553)

• Example2: 更加复杂点的

input = torch.tensor(
        [[0.3, 0.8, 0.5],
        [0.3, 0.3, 0.4],
        [0.3, 0.3, 0.3]
         ], requires_grad=True
)
print('softmax:', torch.softmax(input, dim=1))
target = torch.tensor(  # x
        [0, 2, 1], dtype=torch.long
)

cross_entropy_loss = nn.CrossEntropyLoss()
output = cross_entropy_loss(input, target)
output.backward()

# print('input: ', input)
# print('target: ', target)
print('output: ', output)

print('input.grad: ', input.grad)

• OUTPUT2

softmax: tensor([[0.2584, 0.4260, 0.3156],
                [0.3220, 0.3220, 0.3559],
                [0.3333, 0.3333, 0.3333]], grad_fn=<SoftmaxBackward>)
output:  tensor(1.1617, grad_fn=<NllLossBackward>)  # -(ln(0.2584)+ln(0.3559)+ln(0.3333)) = 1.1617
input.grad:  tensor([[-0.2472,  0.1420,  0.1052],  # -0.2472=(0.2584-1)/3(为什么除以3见证明最后一句) 0.1420 = 0.4260/3
                    [ 0.1073,  0.1073, -0.2147],
                    [ 0.1111, -0.2222,  0.1111]])

5. BCE Loss(Binary Cross-Entropy)

BCE Loss主要用于二分类模型即是该模型只有两个类别, 其中target需要介于0-1之间，所以在BCELoss之前，input一般为sigmod激活层的输出。其中sigmod的导数和softmax的一样所以也可以使用上面的证明。

也就是说:如果该位置为1，那么导数为-(sigmod后的值-1)/N, 如果该位置值为0，那么导数为-(sigmod后的值)/N

BCE Loss用于二分类或者多标签分类。例如YOLOv3的置信度损失使用的就是BCE Loss

(例如yn表示目标边界框与真实框的iou[正样本取1负样本取0],xn为通过sigmod得到的预测置信度，N为正样本个数)

在YOLOv3中，类别损失也是使用BCE Loss, yn取0或者1，表示预测目标边界框i中是否存在第j类目标，xn为预测值，N为正样本个数

参考

• 公式
  
  

• Example

import torch
import torch.nn as nn

m = nn.Sigmoid()
loss = nn.BCELoss()

input = torch.randn((3, 3), requires_grad=True)
target = torch.empty((3, 3)).random_(2)
output = loss(m(input), target)
output.backward()

print("input", input)
print("sigmod(input)", m(input))
print("target", target)
print("output", output)
print("input.grad", input.grad)

• OUTPUT

input tensor([[-0.7722, -0.0539,  0.1969],
        [-1.8228,  1.5270,  0.7037],
        [-0.9524,  0.3780, -0.0544]], requires_grad=True)
sigmod(input) tensor([[0.3160, 0.4865, 0.5491],
        [0.1391, 0.8216, 0.6690],
        [0.2784, 0.5934, 0.4864]], grad_fn=<SigmoidBackward>)
target tensor([[1., 0., 0.],
        [0., 0., 1.],
        [0., 1., 0.]])
output tensor(0.7116, grad_fn=<BinaryCrossEntropyBackward>)
input.grad tensor([[-0.0760,  0.0541,  0.0610],
        [ 0.0155,  0.0913, -0.0368],
        [ 0.0309, -0.0452,  0.0540]])

• OUTPUT中的output计算方式为

第一个 1*ln(0.3160) + (1-0)*ln(1-0.4865) + (1-0)*ln(1-0.5491)
第二个 (1-0)*ln(1-0.1391) + (1-0)*ln(1-0.8216) + 1*ln(0.6690)
第三个 (1-0)*ln(1-0.2784) + 1*ln(0.5934) + (1-0)*ln(1-0.4864)

然后将这三个算出来的数加起来/9 然后再取负数

• OUTPUT中的input.grad计算公式为

计算公式可以按照Cross-Entropy的推导部分来:
target为1的位置计算为(sigmod(值)-1)/N, target为0的位置计算为(sigmod(值))/N
例如
[[(0.3136 - 1)/9=-0.0760,  0.4865/9=0.0541, 0.5491/9=0.0610],
[0.1391/9=0.0155, 0.8216/9=0.0913, (0.6690-1)/9=-0.0368],
[0.2784/9=0.0309, (0.5934-1)/9=-0.0452, 0.4864/9=0.0540]]

+++++++++++++++++++++++++++++++++++分界线+++++++++++++++++++++++++++++++++++++++++++++++

6. 其他IOU Loss以及Focal Loss

• 之前写的博客：https://www.cnblogs.com/zranguai/p/14587231.html
• 参考blogs1: IoU、GIoU、DIoU、CIoU损失函数的那点事儿
• 参考video1: b站视频