HDU6848改编题(弱化)——客星璀璨之夜（stars）

「 客星璀璨之夜 」（stars）

“

虽然不清楚是不是那两人的力量

在那个风暴肆虐的夜晚，的确有一瞬

真的在那一瞬间，在云破天开的时候

透过空隙中看到的璀璨星空，不知为何倒映眼中不能忘怀

”

——《奇迹召唤星辰》

【题目描述】

小苗望着星空，在高中学习了几年物理后正式成为一名理科生后，她突然脑洞大开： 将星空简化成一个数轴，数轴上有 2n + 1 个位置，分别为 x_1 , x_2 , … , x_2n+1，其中奇 数位置有一个正物质恒星，偶数位置有一颗反物质行星。在这里，我们不考虑天体之间 力的作用。

小苗将发动奇迹的力量，从剩下的反物质行星中随机选择一颗，并随机选择向左或 向右，然后施加一个初速度。显然，当正物质与反物质相撞后，它们会发生湮灭并同时 消失。

当上一个行星湮灭后，小苗会再次发动奇迹的力量，直到不存在行星。可以注意到， 没有行星会永远运动下去。 小苗除了学习了物理外，还学习了概率论，所以她想知道所有行星在湮灭之前的运 动距离之和的期望为多少。但是这对于周老师实在是太难了，所以小苗决定向你求助。 你只需要算出期望值 mod 998244353 的结果。

p.s.：如果你不知道模意义下的期望怎么求，首先期望一定能写成有理数 a/b，在 mod 998244353 意义下存在唯一正整数 b^−1 满足 b × b^−1 ≡ 1 mod 998244353，你只 需要输出 a × b^−1 mod 998244353 的值即可。

【输入格式】

从文件 stars.in 中读入数据。

第一行包含一个正整数 n。接下来一行共 2n + 1 个整数 x_1 , x_2 , … , x_2n+1 表示所有天 体的坐标。保证 xi 递增给出。

【输出格式】

输出到文件 stars.out 中。

输出期望值 mod 998244353 的结果。

【样例 1 输入】

1

1 2 3

【样例 1 输出】

1

【样例 2 输入】

3

1 2 3 4 5 6 7

【样例 2 输出】

332748122

【样例 2 解释】

共存在 3! × 2^3 = 48 种不同的可能性，限于篇幅不列举所有情况，期望值为 13/3 。

【样例 3 输入】

10

0 1 3 6 10 15 21 28 36 45 55 66 78 91 105 120 136 153 171 190 210

【样例 3 输出】

969129126

【数据范围与约束】

对于所有测试点，满足 n ≤ 3000, −10^9 ≤ x_1 < x_2 < ⋯ < x_2n+1 ≤ 10^9。

题解

我们把题意转换一下，相当于每次随机把相邻两颗星球（一正一反）并在一起湮灭，消失，旁边的两颗星球变为相邻。

每个行星都会唯一地运动一段距离，显然每个行星都有概率与n+1颗恒星湮灭，也就是每个行星有n+1种情况，n+1种概率，总的就有n(n+1)种情况，可以直接枚举，复杂度为n^2，只要算出当前行星与每一颗恒星湮灭的概率，再分别乘对应的移动距离，加起来就是总期望了。

假如我们要让左数第 i 个行星与左数第 j 颗恒星相撞，这个概率怎么算 ？

j 在左边或在右边肯定是两种情况，但本质是一样的，概率和距离、方向无关。

那么得满足几个条件，

1. i 朝着 j 的方向合并 （p = 1/2）
2. i ~ j 之间的所有星球得在 i 之前湮灭掉，并且不影响到 j （p = ?）
3. i → j 方向更远处的星球不能影响到 j ，但可以不在 i 之前湮灭 （p = ?）

分别考虑一下2和3吧

条件2

下图的黑点是反物质行星，白点是恒星

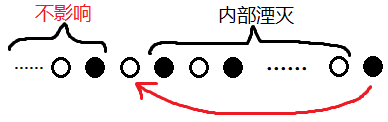
设内部湮灭的中间点总共有 L 对，那么显然他们内部湮灭的概率只跟 L 大小有关，跟距离、位置、甚至方向都无关，

所以设 dp1[i] 为长度为 2i （即中间有 i 对）的连续一段星球互相湮灭的概率（为了不重复考虑，dp1就只要求自己内部不影响外面，而暂不考虑外面对自己的影响），

再设 dp0[i] 为长度为 2i 的连续一段星球互相湮灭，且最外面两个星球最后相撞的概率，

（乘二分之一是因为最外面的那个行星得朝内，乘 i 分之一是因为最外面那个行星得是 i 个行星中最后移动的）

那么简单想一下会发现如下转移：

简单解释一下为什么那里是dp0而不是dp1，

如果是dp1的话，首先他会算重，然后是需要加上自己，会出问题，

枚举 j 实际上是枚举第一个dp0的长度。

好了，我们继续看上面的三个条件，发现前两个条件可以合并一下，用一个包含 i，j 的 dp0 表示，dp1，dp0都可以 n^2 预处理

条件3

这个就比较麻烦了，可以允许两种情况

第一种情况就直接是dp1[j-1]，很简单

第二种情况是笔者做法的重难点，咱们慢慢来

重难点

首先需要强调的是，其中任意一个行星都可以选择在 i 合并之后再出去合并，这样的话，假设该行星为 k

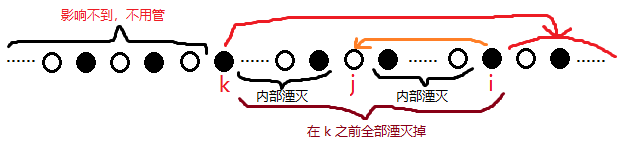
我们发现这个概率居然和 i~k 的总长度有关，而对于每个不同的 k ，i~k 的长度又不一样，那是不是要n^3了呢？

不，绝对不能n^3，

我们发现如果设 dp2[x][y] 为上图 i~j 长度为 2x 、j~k 长度为 2y 时满足 k 最后的概率，那么 dp2 可以 O(1) 转移，

然后预处理一下 dp2[i][1]~dp2[i][j]的前缀和，就可以直接带入了。

本来dp2是要乘那个dp0[i]的，至于转移方程中为什么要打上一个括号，是为了总计算方便，笔者的代码里没有乘它。

复杂度

所有dp都可以预处理，都是n^2，枚举也是n^2的，总复杂度

CODE

#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 6010
#define LL long long
#define DB double
#define ENDL putchar('\n')
//#define int LL
LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s == '-')f = -f;s = getchar();}
	while(s >= '0' && s <= '9') {x = x*10+(s-'0');s = getchar();}
	return f * x;
}
const int jzm = 998244353;
int n,m,i,j,s,o,k,a,b;
int fac[MAXN],inv[MAXN],invf[MAXN],pow2[MAXN],inv2[MAXN];
int C(int n,int m) {return fac[n] *1ll* invf[n-m] % jzm *1ll* invf[m] % jzm;}
int ad[MAXN];
int dp[MAXN],dp0[MAXN],dpr[MAXN>>1][MAXN>>1];//dp1,dp0,dp2/dp0[i]
int main() {
	freopen("stars.in","r",stdin);
	freopen("stars.out","w",stdout);
	n = read();
	pow2[1] = 2;inv2[0] = 1;inv2[1] = 499122177;
	fac[0] = fac[1] = inv[0] = inv[1] = invf[0] = invf[1] = pow2[0] = 1;
	for(int i = 2;i <= (n<<1|1) || i <= 10;i ++) {
		fac[i] = fac[i-1] *1ll* i % jzm;
		inv[i] = (jzm - inv[jzm % i]) *1ll* (jzm / i) % jzm;
		invf[i] = invf[i-1] *1ll* inv[i] % jzm;
		pow2[i] = pow2[i-1] *2ll % jzm;
		inv2[i] = inv2[i-1] *1ll* inv2[1] % jzm;
	}
	dp0[0] = dp[0] = 1;
	for(int i = 1;i <= n;i ++) {
		dp0[i] = dp[i-1] *1ll* inv[i] % jzm *1ll* inv2[1] % jzm;
		dp[i] = dp0[i];
		for(int j = 1;j < i;j ++) {
			(dp[i] += dp[j] *1ll* dp0[i-j] % jzm) %= jzm;
		}
	}
	// !!!必须先处理了dp0和dp1才能处理dp2!!!
	for(int i = 1;i <= n;i ++) {
		for(int j = 1;j+i <= n;j ++) {
			dpr[i][j] = dp[j-1] % jzm *1ll* inv2[1] % jzm *1ll* inv[i+j] % jzm;//由于下面计算概率时乘了个dp0[i]的 ,所以这里不用乘dp0[i]
			(dpr[i][j] += dpr[i][j-1]) %= jzm;
		}
	}
	// 预处理结束 ，可能处理了一些多余的，不过没关系
	for(int i = 1;i <= (n<<1|1);i ++) {
		ad[i] = read();
	}
	// 输入结束
	int tot = fac[n] *1ll* pow2[n] % jzm; //方便调试而已，并没用
	int ans = 0;
	for(int i = 1;i <= n;i ++) {
		for(int j = 1;j <= i;j ++) {
			int p = dp0[i-j+1] *1ll* ((dp[j-1] + dpr[i-j+1][j-1]) % jzm) % jzm;
			(ans += (ad[i<<1] - ad[(j<<1)-1]) % jzm *1ll* p % jzm) %= jzm;
//			printf("(%d -> %d) : %d\n",i,j,p);
		}
		for(int j = i+1;j <= n+1;j ++) {
			int p = dp0[j-i] *1ll* ((dp[n+1-j] + dpr[j-i][n+1-j]) % jzm) % jzm;
			(ans += (ad[(j<<1)-1] - ad[i<<1]) % jzm *1ll* p % jzm) %= jzm;
//			printf("(%d -> %d) : %d\n",i,j,p);
		}
	}
	printf("%d\n",ans);
	return 0;
}