用js简单实现一下迪克斯特拉算法

今天看书看到了迪克斯特拉算法，大概用js实现一下呢，计算最短路径。

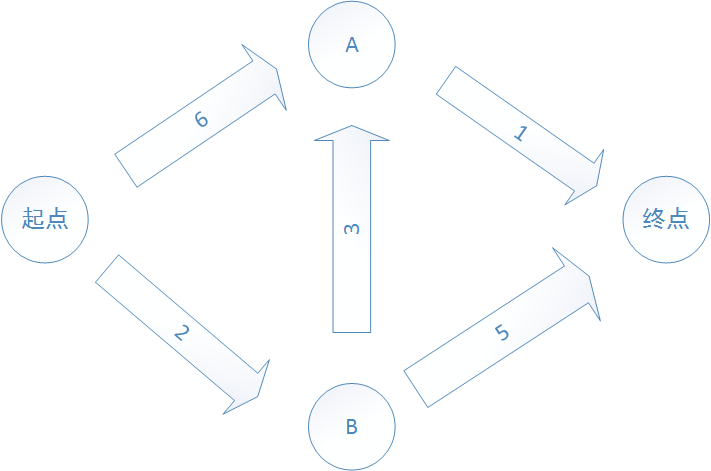
首先，迪克斯特拉算法只适用于有向无环图，且没有负权重，本例关系图如下哦，数字为权重，emmmm，画得稍微有点丑~

　　　　 //大概用js实现一下迪克斯特拉算法，计算最短路径
        // （6）→ A → (1)
        //   ↑    ↑    ↓
        // 起点  (3)  终点
        //   ↓    ↑    ↑
        //  (2) → B → (5)
        //迪克斯特拉算法只适用于有向无环图，且没有负权重
        //上图()内为权重
        //散列表在js中表示为对象
        var graph = {};//记录节点
        graph.start = {};
        graph.start.a = 6;//起点到达A点权重为6
        graph.start.b = 2;

        graph.a = {};
        graph.a.end = 1;
        graph.b = {};
        graph.b.end = 5;
        graph.b.a = 3;

        graph.end = {};

        var costs = {};//记录起点到各点权重
        costs.a = 6;
        costs.b = 2;
        costs.end = '';//暂时不知道

        var parents = {};//记录最短路径中各节点的父节点
        parents.a = 'start';
        parents.b = 'start';
        parents.end = '';

        var processed = {};//记录已处理过的节点

        //找出开销最小的节点(方法比较多呢，随便写了一个)
        function findLowestCostNode(costs) {
            var value = '';
            var node = '';
            for(var key in costs) {
                if(processed[key]) {
                    continue;
                }
                if(!value) {
                    value = costs[key];
                    node = key;
                }else {
                    if(costs[key] && costs[key]<value) {
                        value = costs[key];
                        node = key;
                    }
                }
            }
            return node;
        }

        var node = findLowestCostNode(costs);//找出开销最小节点
        while(node) {
            var cost = costs[node];//当前最小开销
            var neighbors = graph[node];//当前节点相邻节点
            for(var n in neighbors) {
                var newCost = cost + neighbors[n];//到达相邻节点的开销数
                if (!costs[n]) {
                    costs[n] = newCost;
                    parents[n] = node;
                }else {
                    if (costs[n] > newCost) {//检查相应节点开销数是否小于已知开销数
                        costs[n] = newCost;//更新相应节点开销数
                        parents[n] = node;//更新相应节点父节点
                    }
                }
            }
            processed[node] = 1;;//记录已处理过节点
            node = findLowestCostNode(costs);//更新最小节点继续循环
        }

        console.log(costs['end']);//6  此处为最短路径开销
        var line = [];
        line.unshift('end');
        printLine(parents['end']);
        console.log(line);//["start", "b", "a", "end"]

        //使用递归打印出完整路径
        function printLine(node) {
            if( node != 'start') {
                line.unshift(node);
                printLine(parents[node]);
            }else {
                line.unshift('start');
            }
        }

看过的东西不使用就容易忘记，稍微记录一下，写法比较小白，大神们就自动忽略吧~

知道了新东西还真是一件有意思的事情~