神经网络_线性神经网络 1 (Nerual Network_Linear Nerual Network 1)

2019-04-08 16:59:23

1 学习规则(Learning Rule)

1.1 赫布学习规则(Hebb Learning Rule)

1949年，Hebb提出了关于神经网络学习机理的“突触修正”的假设：当神经元的前膜电位、后膜电位同时为正时，突触传导加强；电位相反时，突触传导减弱。根据次假设定义权值ω的调整方法，称该方法为Hebb学习规则。

Hebb学习规则中，学习信号等于神经元的输出：

r=f(W^T_j*X)

权值向量W调整公式：

ΔW=η*f(W^T_j*X)*X

权值向量W的分向量Δω_ij调整公式：

Δω_j=η*f(W^T_j*X)*x_j，j=0,1,2,…,n

为保证Hebb learning rule 的学习效率，对权值设置饱和值。

for examle:

1 参数设置

输入：X¹=[1,-2,1.5]^T、X¹=[1,-0.5,-2]^T、X¹=[0,-1,-1]^T，学习率 η=1，初始化权值W₀=[0 0 0]^T，传递函数使用hardlim。

2 计算步骤(即权值调整过程)

权值W₁=W₀+hardlim(W₀^T*X¹)*X¹=[1 -2 1.5]；

权值W₂=W₁+hardlim(W₁^T*X²)*X²=[1 -2 1.5]；

权值W₃=W₂+hardlim(W₂^T*X³)*X³=[1 -3 0.5]；

1.2 感知器学习规则(Perceptron Leaning Rule)

1 感知器的学习规则

r=d_j-o_j

式中，d_j为期望输出，o_j=f(W_j^T*X)

感知器采用符号函数作为转移函数，则

f(W_j^T*X)=sgn(W_j^T*X)={1，W_j^T*X≥0；0，W_j^T*X<0}

由上式得权值调整公式

ΔW_j=η*[d_j-sgn(W_j^T*X)]*X

Δω_j=η*[d_j-sgn(W_j^T*X)]*x_j

2 Hebb learning principle 和 Perceptron learning principle的不同之处

Hebb learning principle 采用输出结果作为权值调整的组成部分，Perceptron learning principle 采用误差作为权值调整的组成部分。

1.3 最小均方差学习规则(Least Mean Square Error Leaning Rule)

1.3.1 LMS学习规则特点

感知器学习规则训练的网络，其分类的判决边界往往距离各分类模式靠的比较近，这使得网络对噪声比较敏感；

LMS Learing Rule是均方误差最小，进而使得判决边界尽可能远离分类模式，增强了网络的抗噪声能力。

但LMS算法仅仅适用于单层的网络训练，当需要设计多层网络时，需要寻找新的学习算法，for example,Back Progation Nerual Network Algorithm。

1962年，Bernard Widrow 和 Marcian Hoff 提出Widrow-Hoff Learning Princple，该方法的特点是使实际神经元输出与期望输出之间的平方差最小，因此又称为Least Mean Square Erorr Princple。

LMS调整规则应用较为广泛：

1 信号处理

2 BP算法的引领者

1.3.2 LMS学习规则计算

LMS的学习信号

r=t_j-W_j^T*X

权值调整量

ΔW_j=η*(t_j-W_j^T*X)*X

权值分量调整

Δω_j=η*(t_j-W_j^T*X)*x_j，j=0,1,2,...,n

t_j表示期望输出，W_j^T*X表示实际输出

1.3.2 MSE学习规则

均方差(MSE)，是预测数据与原始数据的误差平方的和的均值

MSE=(∑(t_i-a_i)²)/n，其中i=1,2,...,n

Matlab中存在该函数，可以直接调用，e=[1 2 3]，perf=mse(e)=(1²+2²+3²)/n=4.66666667。

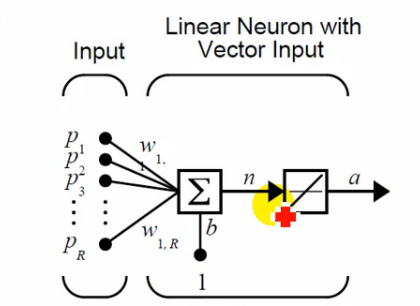
2 线性神经网络

2.1线性神经网路结构

1 参数设置

神经网络结构函数 Purelin