Dijkstra算法的C++实现

Dijkstra算法是在图中寻找两顶点最短路径的算法。

　   下面以下图有向图为例，说明其基本思想。

　

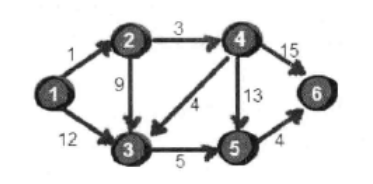
上图为转化为邻接矩阵存储:

    现在我要寻找1点到其他点的最短距离以及路径：

a）1点到各点的距离分别为:  0 1 12 无穷 无穷 无穷

b）从上述距离中寻找最小的距离，发现距离2点最近，那么选择2点作为“跳板”

　c） 1以2作跳板后到各个点的距离分别为（即必走1->2） : 0 1 10 4 无穷 无穷

往后的工作就是重复b） c）继续找最短的距离作为跳板，直到各个点都做过跳板为止。 那么最终这6个数字分别就是顶点1到各个点的最短距离。

有几个问题需要注意：

1. 步骤a）b）找到跳板后再得到c），需要改变的值只是以跳板做中间量后距离变短的值，比如说上述黄色两个部分的第三个位置，加了跳板后是10<没加跳板的12，这时候才需要改成10。假设加了跳板后的值反而比没加前变大了，那么保留原来的值。（这就是的dijkstra的“贪心算法”）。

2. 找跳板的时候只能从没做过跳板中的元素中取。

3.上述方法仅仅讲述了如何求得最短距离，并没有提最短路径，最短路径的实现方法将在过几天的代码中体现。

　　

以下代码以图：

// Dijkstra.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include "stdlib.h"
#define M 999999
int a[][]={,,,,,,,
             ,,,,M,,M,
             ,M,,,M,,M,
             ,,M,,,M,M,
             ,M,,M,,,M,
             ,M,M,M,,,M,
             ,M,M,M,,M, };
int book[];
int dis[];
int i,j,k,u,min;
void dijsktra()
{
    for(i=;i<=;i++)
    {
        dis[i]=a[][i];
        book[i]=;
    }
    book[]=;                                //1点的初始化
    for(i=;i<=;i++)
    {
        min=M;
        for(j=;j<=;j++)
        {
            if(book[j]==&&dis[j]<min)       //找当前最小距离
            {min=dis[j];
                u=j;

            }
        }
        book[u]=;                           for(k=;k<=;k++)                   //若跳板距离更短，那么选择跳板距离作为最短距离  即注1
        {
            if((dis[k])>(a[u][k]+dis[u])&&(a[u][k]<M))  //单独注意a[u][k],表示以u点做跳板，跳板到k的距离 巧妙利用了邻接表
                dis[k]=dis[u]+a[u][k];
        }
    }

    for(i=;i<=;i++)
    {
        printf("%d ",dis[i]);
    }

}

int _tmain(int argc, _TCHAR* argv[])
{
    printf(" \n");
    dijsktra();
    system("pause");
    return ;
}

未完待续，有路径输出的在加着注释 。

参考资料：

https://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html

http://lobert.iteye.com/blog/2315820