poj2689 Prime Distance题解报告

题目戳这里

【题目大意】

给定一个区间[L,R]，求区间内的质数相邻两个距离最大和最小的。

【思路分析】

其实很简单呀，很明显可以看出来是数论题，有关于质数的知识。

要注意一下的就是L和R的数据范围都很大，所以直接跑出1～R的所有质数是不可能的，于是我们就要想办法cut掉一些时间了

然后发现跑出1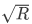～的所有质数是不会超时的，接下来就好办了，直接用这些质数去标记出[L,R]区间内的合数，这样就可以在规定时间内得到[L,R]区间内的质数了，把相邻两质数相减再比较一下就可以得出答案啦QWQ

【代码实现】

这里要说一个问题就是我也不知道为什么我打的代码会TLE掉，虽然我真的jio得和标程没啥差别，所以就一起放上来吧，要是有dalao发现了我的代码问题出在哪里麻烦告知O(∩_∩)O谢谢啦

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 int a[],b[];
 bool v[];
 int n,m,i,j,t1,t2,x1,x2,y1,y2,l,r;
 void prime(){//预处理:埃氏筛法筛素数
     memset(v,,sizeof(v));//初始值都是1,即一开始假设所有的都是质数
     for(i=;i<=;i++)
         if(v[i]){//如果这个数没有被标记过,就说明是质数
             a[++n]=i;//记录质数
             for(j=;j<=/i;j++) v[i*j]=false;
             //把这个质数的倍数都标记为合数
         }
 }
 int main(){
     prime();
     while(cin>>l>>r){
         memset(v,,sizeof(v));
         if(l==) v[]=false;//如果没有这一步的话1会被当做质数处理
         for(i=;i<=n;i++)
             for(j=l/a[i];j<=r/a[i];j++)
                 if(j>) v[a[i]*j-l]=false;
         m=;
         for(i=l;i<=r;i++){
             if(v[i-l]) b[++m]=i;
             if(i==r) break;
         }
         t1=;t2=;
         for(i=;i<m;i++){
             j=b[i+]-b[i];
             if(j<t1) {t1=j;x1=b[i];y1=b[i+];}
             if(j>t2) {t2=j;x2=b[i];y2=b[i+];}
         }
         if(!t2) printf("There are no adjacent primes.\n");
         else printf("%d,%d are closest, %d,%d are most distant.\n",x1,y1,x2,y2);
     }
     return ;
 }

介个是std

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #define go(i,a,b) for(register int i=a;i<=b;i++)
 using namespace std;
 int L,R;
 int prime[];
 int v[];
 bool prim[];
 int l,r,maxn=,maxl,maxr,minn=1e6+,minl,minr;
 int main(){
     int mid=;
     int num=;
     go(i,,mid){//这里我用的线性筛,和std不同
     //但是线性筛不应该比埃氏要快吗？QAQ
         if(v[i]==){
             v[i]=i;prime[++num]=i;
             go(j,,num){
                 if(prime[j]>v[i]||prime[j]>mid/i) break;
                 v[i*prime[j]]=prime[j];
             }
         }
     }
     /*go(i,2,mid){
         if(v[i]==0){
             prime[++num]=i;
             go(j,2,mid/i) v[i*j]=1;
         }
     }*/
     while(cin>>L>>R){
         memset(prim,,sizeof(prim));
         maxn=,minn=1e6+,l=r=;
         if(L==) prim[]=;
         go(i,,num)
             go(j,,R/prime[i]){
                 if(j*prime[i]<L) continue;
                 prim[j*prime[i]-L]=;
             }
         int tot=;
         go(i,,R-L){
             if(prim[i]) {continue;}
             if(l==){l=i+L;tot=;continue;}
             r=i+L;tot++;
             if(r-l>maxn) maxn=r-l,maxl=l,maxr=r;
             if(r-l<minn) minn=r-l,minl=l,minr=r;
             l=r;
         }
         if(tot<) {printf("There are no adjacent primes.\n");}
         else printf("%d,%d are closest, %d,%d are most distant.\n",minl,minr,maxl,maxr);
     }
     return ;
 }

介个是我的TLE代码