LOJ550 Matching 构造

传送门

题意：$T$组询问，每组询问给出一个$N \times M$的网格和一个$K$，每一次你可以消除网格中的两个块，如果两个块的曼哈顿距离小于$K$，则不会得到分数，否则得到等同于它们曼哈顿距离的分数，问最多能得到多少分数。$T \leq 10^5 , N,M \leq 10^6 , K < min(N,M)$

---

我们考虑网格分成四块，从左上到右下边长分别为$\lfloor \frac{M}{2} \rfloor \times \lceil \frac{N}{2} \rceil , \lfloor \frac{N}{2} \rfloor \times \lceil \frac{M}{2} \rceil , \lfloor \frac{N}{2} \rfloor \times \lceil \frac{M}{2} \rceil , \lfloor \frac{M}{2} \rfloor \times \lceil \frac{N}{2} \rceil$，就像下图这样

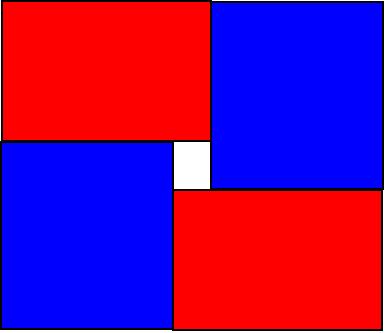
然后红色的和红色的一一匹配，蓝色的和蓝色的一一匹配即可，那么$K$的限制就相当于没有了

所以答案是$\lfloor \frac{M}{2} \rfloor \times \lceil \frac{N}{2} \rceil \times (\lfloor \frac{N}{2} \rfloor + \lceil \frac{M}{2} \rceil) + \lfloor \frac{N}{2} \rfloor \times \lceil \frac{M}{2} \rceil \times (\lfloor \frac{M}{2} \rfloor + \lceil \frac{N}{2} \rceil)$

注意下取整的时候一定要打上括号！！！

 #include<bits/stdc++.h>
 using namespace std;
 int main(){
     int N;
     for(cin >> N ; N ; N--){
         long long L , N , M;
         cin >> N >> M >> L;
         cout << (N / ) * ((M + ) / ) * ((N + ) /  + M / ) + (N + ) /  * (M / ) * (N /  + (M + ) / ) << endl;
     }
     ;
 }