E. Segment Sum（数位dp）

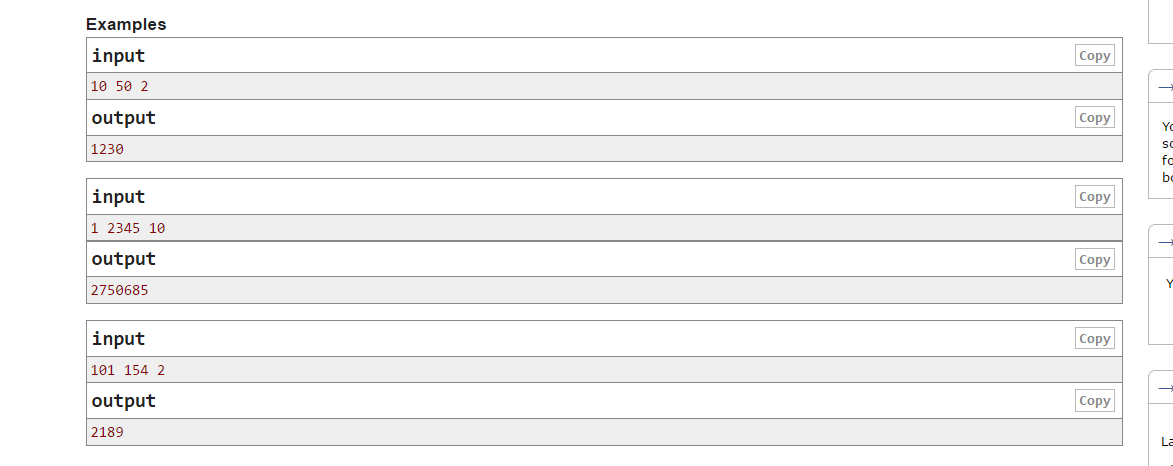
题意：求一个区间内满足所有数位不同数字个数小于K的数字总和。比如：k=2   1,2,3所有数位的不同数字的个数为1满足，但是123数位上有三个不同的数字，即123不满足。

我们可以使用一个二进制的数字来记录某个数字是否已经出现，0为还没有出现，1表示该数字已经出现了。这里还需要注意前导零的干扰。

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<stack>
#include<cstdio>
#include<map>
#include<set>
#include<string>
#include<queue>
using namespace std;
#define inf 0x3f3f3f3f
#define ri register int
typedef long long ll;

inline ll gcd(ll i,ll j){
	return j==0?i:gcd(j,i%j);
}
inline ll lcm(ll i,ll j){
	return i/gcd(i,j)*j;
}
inline void output(int x){
	if(x==0){putchar(48);return;}
	int len=0,dg[20];
	while(x>0){dg[++len]=x%10;x/=10;}
	for(int i=len;i>=1;i--)putchar(dg[i]+48);
}
inline void read(int &x){
    char ch=x=0;
    int f=1;
    while(!isdigit(ch)){
    	ch=getchar();
		if(ch=='-'){
			f=-1;
		}
	}
    while(isdigit(ch))
        x=x*10+ch-'0',ch=getchar();
        x=x*f;
}
struct st{
	ll num;
	ll sum;
	st():num(0),sum(0){
	}
	st(ll num,ll sum):num(num),sum(sum){
	}
}dp[20][2000];
int maxs;
int a[20];
const ll mod=998244353;
int change(int n){
	int cnt=0;
	while(n){
		if(n&1)cnt++;
		n/=2;
	}
	return cnt;
}
st dfs(int pos,int sta,int pre,bool limit){
	if(pos==-1){
	//	cout<<pre<<endl;

		if(change(sta)<=maxs)
		return st(1,0);
		return st(0,0);
	}
	if(dp[pos][sta].num!=0&&!limit){
	//	printf("%d %lld\n",pos,dp[pos][sta].sum);
		return dp[pos][sta];
	}
	int up=limit?a[pos]:9;
	st ans;	

	for(int i=0;i<=up;i++){
		st tem;
		if(change(sta|(int)pow(2,i))>maxs)
		continue;
		if(pre==0&&i==0){
			 tem=dfs(pos-1,sta,0,i==up&&limit);
		}
		else{
			tem=dfs(pos-1,((int)pow(2,i))|sta,i,i==up&&limit);
		}
		ans.num+=tem.num;
		ans.num=ans.num%mod;
	ans.sum=(ans.sum+(ll)pow(10,pos)%mod*i*tem.num%mod+tem.sum)%mod;
	}
	if(!limit){
		dp[pos][sta]=ans;
	}
	return ans;
}
ll solve(ll n){
	int len=0;
	while(n){
		a[len++]=n%10;
		n/=10;
	}
	return dfs(len-1,0,0,true).sum;
}
int main(){
	ll l,r;
	scanf("%lld%lld%d",&l,&r,&maxs);
	printf("%lld",(solve(r)-solve(l-1)+mod)%mod);
	return 0;
}