Gym 102056L - Eventual … Journey - [分类讨论][The 2018 ICPC Asia-East Continent Final Problem L]

题目链接：https://codeforces.com/gym/102056/problem/L

LCR is really an incredible being.

Thinking so, sitting on the plane and looking at the sea, Rikka savours the fantastic journey. A fire never happened. It must be interesting to share it with her mates, and another travel is also fascinating.

But before all, home is the best.

She travels by the JR lines. There are n stations in total, and m public bidirectional railway lines are built among them. Each station belongs to either JR West or JR East. Both JR West and JR East have their own private railways connecting all stations owned by themselves.

Rikka has some through tickets and two types of special passes: ICOCA for JR West and Suica for JR East. She pays a through ticket each time and does one of the following:

Travel from one terminal to another via a public railway line.
Travel to any station which has the same owner as the current one, using one of her special passes. A pass can be used for multiple times.
Rikka wonders, for each start station, the sum of the minimal numbers of tickets she needs to pay to reach every possible one of the other stations.

Input
The first line contains two integers $n,m (1 \le n \le 10^5,0 \le m \le 10^5)$, the numbers of stations and public railways.

The next line contains $n$ integers $A_i (A_i \in {0,1},i=1,2,…,n)$, separated by spaces, describing the owner of each station. $A_i=0$ if the station $i$ belongs to JR west, and vice versa.

The following $m$ lines describe all the public railways, each of which contains two integers $u,v (1 \le u,v \le n,u \neq v)$, representing a bidirectional railway connecting $u$ and $v$. It is guaranteed that no two public railways connect the same pair of stations, and Rikka is able to travel between every pair of stations. Notice that the private railways are not given directly in the input, and Rikka may have to use her passes rather than traveling only through the public railways.

Output
Output $n$ integers in one line, separated by spaces. The $i$-th integer is $\sum_{j=1}^{n}D(i,j)$ , where $D(u,v)$ is the minimal number of tickets needed to travel from $u$ to $v$.

Examples
input
3 2
1 0 0
1 2
1 3
output
2 2 2
input
5 3
1 0 1 0 1
1 2
2 3
4 5
output
5 5 5 6 5

题意：

有 $n$ 个车站，相互之间有 $m$ 条公共的双向铁路连通，车站分成 $0,1$ 两种类别，任意两个 $0$ 类车站之间都有一条私有的铁路相互连接，$1$ 类车站也类似。

现在，从每车站 $i$ 出发，到车站 $j$ 的最少走过的铁路数目为 $D(u,v)$，要求你对每个固定的车站 $i$，都输出到其他所有车站的 $D(i,j)$ 之和。

题解：

首先，任意两个同类车站之间肯定只需要走一步即可到达。而异类车站则有三种可能：一种是和当前车站有公共铁路连接可一步到达、一种是走两步到达、一种是走三步到达（如下图）。

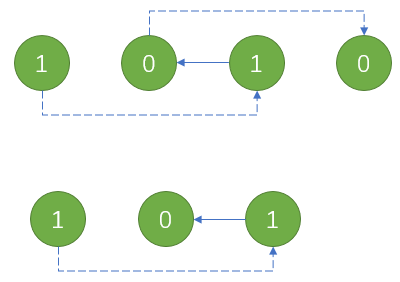
不妨设我现在出发点是个 $1$ 类车站，统计一下同类车站的数目，这些车站是一步直达的；

其次，我分成三类统计异类车站：

　　1、从当前车站出发，通过公共铁路一步直达；

　　2、有另外一个 $1$ 类车站和其有公共铁路相连，这种必然是两步到达；

　　3、没有 $1$ 类车站和其之间存在公共铁路，（这种车站，走三步到达还是走两步到达要取决于当前车站，看当前车站有没有公共铁路直连异类车站）。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+;
int n,m,type[maxn],tag[maxn];
//type[i]:车站类型
//tag[i]:记录有多少个异类车站和其直接相连
int cnt[][];
//cnt[1][0]:有0类车站和其相连的1类车站数目
//cnt[1][1]:无0类车站和其相连的1类车站数目
//cnt[0][0]:无1类车站和其相连的0类车站数目
//cnt[0][1]:有1类车站和其相连的0类车站数目
int main()
{
    cin>>n>>m;
    for(int i=;i<=n;i++) scanf("%d",&type[i]);

    memset(tag,,sizeof(tag));
    for(int i=,u,v;i<=m;i++)
    {
        scanf("%d%d",&u,&v);
        if(type[u]!=type[v]) tag[u]++, tag[v]++;
    }

    memset(cnt,,sizeof(cnt));
    for(int i=;i<=n;i++)
    {
        if(type[i])
        {
            if(tag[i]) cnt[][]++;
            else cnt[][]++;
        }
        else
        {
            if(tag[i]) cnt[][]++;
            else cnt[][]++;
        }
    }
    //printf("cnt10=%d cnt11=%d cnt01=%d cnt00=%d\n",cnt[1][0],cnt[1][1],cnt[0][1],cnt[0][0]);

    for(int i=,ans;i<=n;i++)
    {
        if(i>) printf(" ");
        if(type[i])
        {
            ans=(cnt[][]+cnt[][]-)+tag[i]; //一步
            ans+=(cnt[][]-tag[i])*; //两步
            ans+=cnt[][]*(tag[i]?:); //两步or三步
            printf("%d",ans);
        }
        else
        {
            ans=(cnt[][]+cnt[][]-)+tag[i]; //一步
            ans+=(cnt[][]-tag[i])*; //两步
            ans+=cnt[][]*(tag[i]?:); //两步or三步
            printf("%d",ans);
        }
    }
}