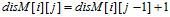NLP-最小编辑距离
最小编辑距离
一 概念
编辑距离(Edit Distance),又称Levenshtein距离,是指两个字串之间,由一个转成另一个所需的编辑操作次数。最小编辑距离,是指所需最小的编辑操作次数。
编辑操作包含:插入、删除和替换三种操作。
二 最小编辑距离解法-动态规划解法
动态规划的核心思想是:将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
由于动态规划解决的问题多数有重叠子问题这个特点,为减少重复计算,对每一个子问题只解一次,我们将其不同阶段的不同状态保存在一个二维数组中。
最小编辑距离算法伪代码:
输入:字符串1-str1 字符串2-str2
输出:最小编辑距离
实质问题:
求解动态规划矩阵。假设我们以str1为主串(即对str1进行操作)
算法:
- 假设str1=ABCD str2=ACD;len1=str1的长度,len2为str2的长度。
- 建立矩阵:
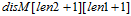
#
A
B
C
D
#
A
C
D
#表示在串前可以插入任何字符。
- 初始化:
#
A
B
C
D
#
0
1
2
3
4
A
1
C
2
D
3
- 三种编辑操作对应着矩阵的三种走法:
|
矩阵方向 |
编辑操作 |
计算公式 |
|
向右走:Right |
删除 |
|
|
向下走:Down |
插入 |
|
|
对角线:Diagonal |
替换|匹配 |
|
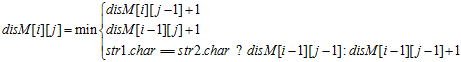
循环计算整个矩阵
|
# |
A |
B |
C |
D |
|
|
# |
0 |
1 |
2 |
3 |
4 |
|
A |
1 |
0 |
1 |
2 |
3 |
|
C |
2 |
1 |
1 |
1 |
2 |
|
D |
3 |
2 |
2 |
2 |
1 |
5.  即为最小编辑距离
即为最小编辑距离
三 应用
最小编辑距离通常作为一种相似度计算函数被用于多种实际应用中,详细如下:(特别的,对于中文自然语言处理,一般以词为基本处理单元)
- 生物领域中DNA分析:比较 DNA 序列并尝试找出两个序列的公共部分。如果两个 DNA 序列有类似的公共子序列,那么这些两个序列很可能是同源的。在比对两个序列时,不仅要考虑完全匹配的字符,还要考虑一个序列中的空格或间隙(或者,相反地,要考虑另一个序列中的插入部分)和不匹配,这两个方面都可能意味着突变(mutation)。在序列比对中,需要找到最优的比对(最优比对大致是指要将匹配的数量最大化,将空格和不匹配的数量最小化)。
- NLP中应用:即两个字符串的相似计算函数可用于下面的任务。
- 拼写纠错(Spell Correction):又将每个词与词典中的词条比较,英文单词往往需要做词干提取等规范化处理,如果一个词在词典中不存在,就被认为是一个错误,然后试图提示N个最可能要输入的词——拼写建议。常用的提示单词的算法就是列出词典中与原词具有最小编辑距离的词条。
- 命名实体抽取(Named Entity Extraction):由于实体的命名往往没有规律,如品牌名,且可能存在多种变形、拼写形式,这样导致基于词典完全匹配的命名实体识别方法召回率较低,为此,我们可以使用编辑距离由完全匹配泛化到模糊匹配,先抽取实体名候选词。
- 实体共指(Entity Coreference):通过计算任意两个实体名之间的最小编辑距离判定是否存在共指关系。
- 字符串核函数(String Kernel):最小编辑距离作为字符串之间的相似度计算函数,用作核函数,集成在SVM中使用。
NLP-最小编辑距离的更多相关文章
- stanford NLP学习笔记3:最小编辑距离(Minimum Edit Distance)
I. 最小编辑距离的定义 最小编辑距离旨在定义两个字符串之间的相似度(word similarity).定义相似度可以用于拼写纠错,计算生物学上的序列比对,机器翻译,信息提取,语音识别等. 编辑距离就 ...
- 【NLP_Stanford课堂】最小编辑距离
一.什么是最小编辑距离 最小编辑距离:是用以衡量两个字符串之间的相似度,是两个字符串之间的最小操作数,即从一个字符转换成另一个字符所需要的操作数,包括插入.删除和置换. 每个操作数的cost: 每个操 ...
- C#实现Levenshtein distance最小编辑距离算法
Levenshtein distance,中文名为最小编辑距离,其目的是找出两个字符串之间需要改动多少个字符后变成一致.该算法使用了动态规划的算法策略,该问题具备最优子结构,最小编辑距离包含子最小编辑 ...
- lintcode:最小编辑距离
最小编辑距离 给出两个单词word1和word2,计算出将word1 转换为word2的最少操作次数. 你总共三种操作方法: 插入一个字符 删除一个字符 替换一个字符 样例 给出 work1=&quo ...
- 自然语言处理(5)之Levenshtein最小编辑距离算法
自然语言处理(5)之Levenshtein最小编辑距离算法 题记:之前在公司使用Levenshtein最小编辑距离算法来实现相似车牌的计算的特性开发,正好本节来总结下Levenshtein最小编辑距离 ...
- POJ 3356 AGTC(最小编辑距离)
POJ 3356 AGTC(最小编辑距离) http://poj.org/problem?id=3356 题意: 给出两个字符串x 与 y,当中x的长度为n,y的长度为m,而且m>=n.然后y能 ...
- Minimum edit distance(levenshtein distance)(最小编辑距离)初探
最小编辑距离的定义:编辑距离(Edit Distance),又称Levenshtein距离.是指两个字串之间,由一个转成还有一个所需的最少编辑操作次数.许可的编辑操作包含将一个字符替换成还有一个字符. ...
- 牛客寒假算法基础集训营2 【处女座与复读机】DP最小编辑距离【模板题】
链接:https://ac.nowcoder.com/acm/contest/327/G来源:牛客网 一天,处女座在牛客算法群里发了一句“我好强啊”,引起无数的复读,可是处女座发现复读之后变成了“处女 ...
- 最小编辑距离python
1 什么是编辑距离在计算文本的相似性时,经常会用到编辑距离(Levenshtein距离),其指两个字符串之间,由一个字符串转成另一个所需的最少编辑操作次数.在字符串形式上来说,编辑距离越小,那么两个文 ...
- 通俗解析莱文斯坦距离(Levenshtein Distance)计算原理(最小编辑距离)
[版权声明]:本文章由danvid发布于http://danvid.cnblogs.com/,如需转载或部分使用请注明出处 最近看到一些动态规划的东西讲到莱文斯坦距离(编辑距离)的计算,发现很多都讲的 ...
随机推荐
- Memcahed服务异常监控脚本
#!/bin/sh # filename: mon_mc.sh export MemcahedIp=$1export MemcahedPort=$2export NcCmd="nc $Mem ...
- ANDROID常用的命令(转载,后续自己完善)
1.adb devices:查看当前已连接的设备.2.adb shell:进入android的shell模式.3.echo 3>/proc/sys/vm/drop_caches:清除一下系统的c ...
- codeforces 427 div.2 F. Roads in the Kingdom
F. Roads in the Kingdom time limit per test 2 seconds memory limit per test 256 megabytes input stan ...
- px与与rem vw的区别
1.px 使用具体像素点为单位,好处是比较稳定和精确,但在浏览器放大缩小会出现问题 2.rem 参考根元素的值 例如设置根元素字体大小是20像素 在h1中设置字体大小 那么H1的大小就是40px p的 ...
- xmlUtil 解析 创建
http://yangzi09150915.blog.163.com/blog/static/32953487201072911410398/ package com.aibi.cmdc.webSer ...
- 【Atheros】Iperf性能测试的问题小结
1. Iperf用文件作为数据源无效的问题 2. 在代码中修改iperf数据,iperf无法收到,但在mac层能拿到数据 3. TCP发不出去包的问题 1. Iperf用文件作为数据源无效的问题 Ip ...
- 【问题】:spring cloud sleuth日志组件冲突问题
在使用spring cloud sleuth的时候,启动工程报错如下: 根据错误信息明显就是jar包冲突,spring boot默认用的是logback,所以移除其中一个依赖就可以了,修改pom依赖为 ...
- Android分享图片失败解决方案
前言:在做图片分享到微博或是用彩信分享的时候,会遇到“无法将图片添加到信息中”,其实这个问题的原因是创建的那个图片默认是,只能被当前应用调用,无法被其他应用调用,即分享的时候,无法读取到图片,并提示I ...
- iOS将Unity导出的Xcode工程导入到另一个Xcode项目, 及常见报错的解决方法
demo下载地址 http://pan.baidu.com/s/1pLcpKpl 1.Unity导出工程时设置bundle id要与项目一致 2.修改bit code为NO 3.删除Main.stor ...
- G - 湫湫系列故事——减肥记I
G - 湫湫系列故事——减肥记I Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u De ...