Searching a 2D Sorted Matrix Part I

Write an efficient algorithm that searches for a value in an n x m table (two-dimensional array). This table is sorted along the rows and columns — that is,

Table[i][j] ≤ Table[i][j + 1], 
Table[i][j] ≤ Table[i + 1][j]

Solution:

1. STEP 方法：

Start in the bottom-left corner of your matrix. Then go to the right until you find the exact number (done), or until you find a number that is bigger.

Then you go upwards in the matrix until you find the exact number (done), or until you find a number that is too small.

Then again you move to the right, ... and so on until you found the number or until you reach the right-side or top of your matrix.

The following images contain some examples, using an Excel table showing the target number in green, and the path that is followed in yellow.

In the last example we look for 207, which isn't in the matrix:

This is just the algorithm. The coding is left for you as an exercise :-)

EDIT: When starting on the bottom row, a binary search might give a better starting point. For the rest of the algorithm it probably doesn't matter.

Step-wise Linear Search:
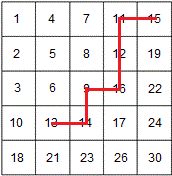
We call this the Step-wise Linear Search method. Similar to Diagonal Binary Search, we begin with the upper right corner (or the bottom left corner). Instead of traversing diagonally each step, we traverse one step to the left or bottom. For example, the picture below shows the traversed path (the red line) when we search for 13.

Essentially, each step we are able to eliminate either a row or a column. The worst case scenario is where it ended up in the opposite corner of the matrix, which takes at most 2n steps. Therefore, this algorithm runs in O(n) time, which is better than previous approaches.

 

An example showing the traversed path using step-wise linear search (colored in red) when the target element is 13.

Below is the code and it is simple and straight to the point. You should not make any careless mistake during the interview.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

boolstepWise(intmat[][N_MAX],intN,inttarget,               int&row,int&col){   if(target<mat[0][0]||target>mat[N-1][N-1])returnfalse;   row=0;   col=N-1;   while(row<=N-1&&col>=0){     if(mat[row][col]<target)       row++;     elseif(mat[row][col]>target)       col--;     else       returntrue;   }   returnfalse; }

This is probably the answer that most interviewers would be looking for. But we will not stop here. Let us continue exploring some more interesting solutions.

2. 分治。

Quad Partition:
Did you realize that this problem is actually solvable using a divide and conquer approach? I bet you did!

First, we make an observation that the center element always partition the matrix into four smaller matrices. For example, the center element 9 partitions the matrix into four matrices as shown in the picture below. Since the four smaller matrices are also sorted both row and column-wise, the problem can naturally be divided into four sub-problems.

If you notice carefully, we are always able to eliminate one of the four sub-problems in each step. Assume our target is21, which is greater than the center element 9. We can eliminate the upper left quadrant instantly, because all elements in that quadrant are always less than or equal to 9. Now assume our target is 6, which is less than 9.

Similarly, we eliminate the bottom right quadrant from consideration, because elements in that quadrant must all be greater than 9. Please note however, we still need to search the upper right and bottom left quadrant, even though the example below seems to show all elements in the two mentioned quadrants are greater than 9.

Of course, if the center element is our target element, we have found the target and stop searching. If not, we proceed by searching the rest of three quadrants.

The center element 9 partitions the matrix into four smaller quadrants (shown as four different colors).

What’s the complexity of the Quad Partition method? As it turns out, the run time complexity could be written directly as a recurrence relation:

 T(n) = 3T(n/2) + c,
 
 where n is the dimension of the matrix.

We add a constant c because each step we do a comparison between the target element and the center element, which takes some constant time.

We need to solve the above equation to obtain the complexity. This is where most confusion comes in. If you have taken advanced algorithm course, you could solve it using the Master’s theorem, but you don’t really need to. You could just expand the recurrence relation directly to solve it.

Below is the code for the Quad Partition method. l and u represents the upper left corner, while r and d represents the bottom right corner of the matrix. Be very careful of corner cases. Please note that the code below checks for when lequals r (left = right) and u equals d (up = down) (ie, the matrix has only one element). If this only element differs from the target, the function must return false. If you omit this condition, then the code below never terminates, which in other word translates to: You never double check your code, and it is Hasta la vista, baby from your interviewer.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

boolquadPart(intmat[][N_MAX],intM,intN,inttarget,intl,intu,intr,intd,int&targetRow,int&targetCol){   if(l>r||u>d)returnfalse;   if(target<mat[u][l]||target>mat[d][r])returnfalse;   intcol=l+(r-l)/2;   introw=u+(d-u)/2;   if(mat[row][col]==target){     targetRow=row;     targetCol=col;     returntrue;   }elseif(l==r&&u==d){     returnfalse;   }   if(mat[row][col]>target){     returnquadPart(mat,M,N,target,col+1,u,r,row,targetRow,targetCol)||            quadPart(mat,M,N,target,l,row+1,col,d,targetRow,targetCol)||            quadPart(mat,M,N,target,l,u,col,row,targetRow,targetCol);   }else{     returnquadPart(mat,M,N,target,col+1,u,r,row,targetRow,targetCol)||            quadPart(mat,M,N,target,l,row+1,col,d,targetRow,targetCol)||            quadPart(mat,M,N,target,col+1,row+1,r,d,targetRow,targetCol);   } }   boolquadPart(intmat[][N_MAX],intN,inttarget,int&row,int&col){   returnquadPart(mat,N,N,target,0,0,N-1,N-1,row,col); }

3.Binary Partition:

We can even reduce the number of sub-problems from three to only two using a method we called Binary Partition. This time we traverse along either the middle row, middle column, or diagonally (as shown in highlighted gray cells in imagesa), b), and c) below). As we traverse, we find the point such that the target element s satisfies the following condition:

 ai < s < ai+1, where ai is the i

^th

 traversed cell.

a) Row-wise binary partition. The highlighted gray cells represents the traversed row (the middle row). The target 10 is found between 9 and 16.

b) Column-wise binary partition. The highlighted gray cells represents the traversed column (the middle column). The target 10 is found between 9 and 14.

c) Diagonal-based binary partition. The highlighted gray cells represents the traversed diagonal. The target 10 is found between 9 and 17. Please note that diagonal-based binary partition would fail in a non-square matrix (for the above example, it will not work in the two sub-matrices because they are non-square matrices).

If the target element equals one of the traversed cells, we immediately return the element as found. Otherwise we partition the matrix into two sub-matrices following the partition point we found. As it turns out, we need cn time (linear time) to find such partition point, since we are essentially performing a linear search. Therefore, the complexity could be written as the following recurrence relation: (Note: I omitted the proof, as it is left as an exercise to the reader.  )

 T(n) = 2T(n/2) + cn
      = O(n lg n)

The Binary Partition algorithm runs in O(n lg n) time. You might expect its complexity to be lower than Quad Partition, since it has only two sub-problems (instead of three) to solve. The reason of the higher order complexity is due to the extra O(n) time doing a linear search for the partition point where a_i < s < a_i+1.

Please note that the matrix is not necessarily divided into two equal-sized sub-matrices. One of the matrix could be bigger than the other one, or in the extreme case, the other matrix could be of size zero. Here, we have made an assumption that each partition step divides the matrix into two equal-sized sub-matrices, just for the sake of complexity analysis.

Below is the code for the Binary Partition method. The code below chooses the middle column as the place to search for the partition point.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

boolbinPart(intmat[][N_MAX],intM,intN,inttarget,intl,intu,intr,intd,int&targetRow,int&targetCol){   if(l>r||u>d)returnfalse;   if(target<mat[u][l]||target>mat[d][r])returnfalse;   intmid=l+(r-l)/2;   introw=u;   while(row<=d&&mat[row][mid]<=target){     if(mat[row][mid]==target){       targetRow=row;       targetCol=mid;       returntrue;     }     row++;   }   returnbinPart(mat,M,N,target,mid+1,u,r,row-1,targetRow,targetCol)||          binPart(mat,M,N,target,l,row,mid-1,d,targetRow,targetCol); }   boolbinPart(intmat[][N_MAX],intN,inttarget,int&row,int&col){   returnbinPart(mat,N,N,target,0,0,N-1,N-1,row,col); }

4.

Improved Binary Partition: 在遍历中间那一row / column 时使用二分 来找。
Since the partition column (or row, or diagonal) is sorted, not utilizing the sorted configuration is a waste. In fact, we are able to modify binary search to search for the partition point in lg n time. Then, the complexity can be expressed as the following recurrence relation: (Note: I’ve omitted some steps, try to work out the math by yourself)

By incorporating binary search, we are able to reduce the complexity to O(n). However, we have made an assumption, that is: Each subdivision of matrices must be of equal size (or, each partition point is exactly at the center of the partition column). This leads to the following question:

It is entirely possible that the subdivided matrices are of different sizes. Would the complexity change by an order in this case?

This turns out to be a difficult question to answer, but I could provide further insight to you by deriving the complexity of the other extreme, that is:

Each subdivision results in only one sub-matrix (ie, one matrix has the original matrix being halved, while the other matrix is empty.)

For an example of the above case, try searching for –1 in the above sample matrix shown in image (a). Since each subdivision results in the original matrix being halved, the total number of subdivisions can be at most lg n times. Assuming each binary search performed before a subdivision takes c lg n time, the complexity can be expressed as follow:

As you can see, the run time complexity of this extreme case is O(lg n)², which turns out to be even less than O(n). We conclude that this is not the worst case scenario, as some people might believe.

Please note that the worst case for the Improved Binary Partition method had not been proven here. We had merely proven that one case of the Improved Binary Partition could run in O(n). If you know the proof of the worst case, I would be interested to hear from you.

Next Problem：

2D Matrix(n * n) of positive and negative numbers is given. Matrix is sorted rowwise and columnwise. You have to return the count of -ve numbers in most optimal way.