UVA 1659 Help Little Laura 帮助小劳拉 (最小费用流，最小循环流)

（同时也是HDU 2982，UVA的数据多）

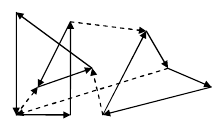
题意：平面上有m条有向线段连接了n个点。你从某个点出发顺着有向线段行走，给走过的每条线段涂一种不同的颜色，最后回到起点。你可以多次行走，给多个回路涂色（要么不涂色，要么就至少给一个回路上的边全部涂色）。可以重复经过一个点，但不能重复经过一条有向线段。如下图所示的是一种涂色方法（虚线表示未涂色，即每次都可以从任意点出发染色）。每涂一个单位长度将得到X分，但每使用一种颜色将扣掉Y分。假设你拥有无限多种的颜色，问如何涂色才能使得分最大？输入保证若存在有向线段u -> v，则不会出现有向线段v -> u。

　　n <= 100，m <= 500，1 <= X，Y <= 1000。

　　对于坐标（x，y）0 <= x，y <= 1000。

 

 

 

 

 

思路：看刘汝佳的书的第二种方法，再参考这篇博文才把代码长度降下来了。http://blog.csdn.net/u013368721/article/details/30553815

 

　　要求的就是最大费用循环流（即每找到一个环就可以进行增广）。找环可能并不复杂，但是要找一个最大的环就有点复杂了，所以用网络流解决。又因为找的是最大费用，按老套路的话会出现无限增大费用的情况，所以要先将每条边的费用取相反数（前面加个负），才可以有机会求最小费用流。而这些边的权有正有负，取完之后也可能出现负环了，所以主要问题就是解决负环。

　　用最小费用流求最大费用循环流时，解决负环的一种方法：

（1）先将所有边权取反。

（2）建边。正权值的边容量为1，费用为权值。负权值的边u->v拆成3条边，分别是S->v，v->u，u->T，容量都为1，v->u费用为负权的相反数，其他2条费用为0。这样会出现某个点有多条边连到S或T，可以互相抵消到一方为0为止，统计剩下多少条k，将其中1条的容量设为k，其他的全部删掉。如果全部抵消掉了，那就将连S和T的边全部删掉。（这个删边的方法有技巧）

（3）跑一次最小费用流得到的总费用，加上所有负权之和之后（注：此时答案已为负的），再取反即得到最大费用。

 

 

　　删边技巧是，在建这S->v，v->u，u->T 三条边时，先建中间那条，统计该点连到S几次，减去连到T点几次，结果若为正，则与S连一条边，容量就是几次，若负，同理。

 

　　至于why it works！得好好想想~

　　画几个点验证了一下发现，如果一个原图中的环（权值大于0）值得取，那么流会自动流向该环原图中的负权边。而如果不值得取，那么会流向原图中的正权边。因为我们是用sum（负值）加上那个费用（正值），所以当该环要取时，则自动减去那些负权，不取呢，会自动减去那些正权（而那些负权的完全没取到）。不懂就画个环出来验证吧。

 

 

 

 

 

 

 #include <bits/stdc++.h>
 #define LL long long
 #define pii pair<int,int>
 #define pdi pair<double,int>
 #define INF 0x7f7f7f7f
 using namespace std;
 const int N=;
 int x[N], y[N], rudu[N];
 int earn, lost, n;
 vector<int> vect[N], vec[N];
 double sum;

 struct node
 {
     int from, to, cap, flow;
     double val;
     node(){};
     node(int from,int to,double val,int cap,int flow):from(from),to(to),val(val),cap(cap),flow(flow){};
 }edge[];
 int edge_cnt;

 void add_node(int from,int to,double val,int cap,int flow)
 {
     edge[edge_cnt]=node(from, to, val, cap, flow );
     vec[from].push_back(edge_cnt++);
 }

 void build_graph()
 {
     for(int i=; i<=n; i++)
     {
         for(int j=; j<vect[i].size(); j++)
         {
             int t=vect[i][j];
             double v= lost - sqrt( pow(x[i]-x[t],)+pow(y[i]-y[t],) )*earn;

             if(v<)
             {
                 add_node(t, i, -v, ,  );  //反边
                 add_node(i, t, v, ,  );
                 sum+=v;
                 rudu[t]++,rudu[i]--;
             }
             else
             {
                 add_node(i, t, v, , );
                 add_node(t, i, -v, , );
             }
         }
     }
     for(int i=; i<=n; i++)
     {
         if(rudu[i]>)
         {
             add_node(, i, , rudu[i], );
             add_node(i, , , , );
         }
         if(rudu[i]<)
         {
             add_node(i, n+, , -rudu[i], );
             add_node(n+, i, , , );
         }
     }
 }

 int flow[N], path[N], inq[N];
 double cost[N];

 double spfa(int s,int e)
 {
     deque<int> que(,s);
     cost[s]=;
     flow[s]=INF;
     inq[s]=;
     while(!que.empty())
     {
         int x=que.front();
         que.pop_front();
         inq[x]=;
         for(int i=; i<vec[x].size(); i++)
         {
             node e=edge[vec[x][i]];
             if(e.cap>e.flow && cost[e.to]>cost[e.from]+e.val )
             {
                 flow[e.to]=min(flow[e.from],e.cap-e.flow);
                 cost[e.to]=cost[e.from]+e.val;
                 path[e.to]=vec[x][i];
                 if(!inq[e.to])
                 {
                     inq[e.to]=;
                     que.push_back(e.to);
                 }
             }
         }
     }
     return cost[e];
 }

 double mcmf(int s,int e)
 {
     double ans_cost=0.0;
     while(true)
     {
         memset(flow,,sizeof(flow));
         memset(inq,,sizeof(inq));
         memset(path,,sizeof(path));
         for(int i=; i<=e; i++)   cost[i]=1e39;

         double tmp=spfa(s,e);    //返回费用
         if(tmp>1e38)    return  ans_cost;
         ans_cost+=tmp;

         int ed=e;
         while(ed!=s)
         {
             int t=path[ed];
             edge[t].flow+=flow[n+];
             edge[t^].flow-=flow[n+];
             ed=edge[t].from;
         }
     }
 }

 int main()
 {
     freopen("input.txt", "r", stdin);
     int b, j=;
     while(scanf("%d", &n), n)
     {
         scanf("%d%d",&earn,&lost);
         for(int i=; i<=n+; i++)   vect[i].clear();
         for(int i=; i<=n+; i++)   vec[i].clear();
         memset(edge,,sizeof(edge));
         memset(rudu,,sizeof(rudu));
         edge_cnt=;
         sum=;

         for(int i=; i<=n; i++)
         {
             scanf("%d%d",&x[i],&y[i]);
             while(scanf("%d",&b), b)    vect[i].push_back(b);   //原图邻接表
         }
         build_graph();
         printf("Case %d: %.2f\n", ++j,  -(mcmf(,n+)+sum)+0.0000001 );
     }
     return ;
 }

AC代码