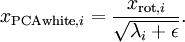Deep Learning 学习笔记(9):主成分分析( PCA )与 白化( whitening )
废话:
这博客有三个月没更新了。
三个月!!!尼玛我真是够懒了!!
这三个月我复习什么去了呢?
托福…………
也不是说我复习紧张到完全没时间更新,
事实上我甚至有时间打LOL。
只是说,我一次就只能(只想?)做一件事情。
对我来说,在两种不同思维之间转换是十分耗费能量的。
说白了我!就!是!个!废!柴!……哼……
前言:
PCA与白化,
就是对输入数据进行预处理,
前者对数据进行降维,后者对数据进行方差处理。
虽说原理挺简单,但是作用可不小。
之前的师兄做实验的时候,就是忘了对数据预处理,
结果实验失败了。
可见好的PCA对实验结果影响挺重要。
主成成分分析(PCA):
主要思想(我总结的):
通过抛弃携带信息量较少的维度对数据进行降维处理,从而加速机器学习进程。
方法:
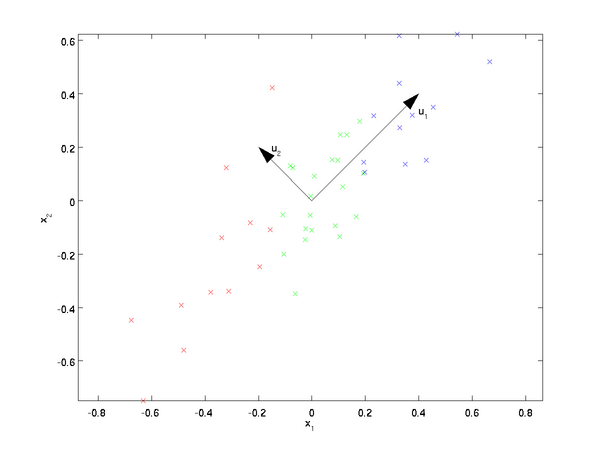
一、数据的旋转(其实我觉着,这个有点像向量正交化的过程)
1、使用的输入数据集表示为 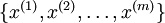
2、首先计算出协方差矩阵 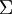 ,如下所示:
,如下所示:
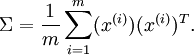
可以证明,数据变化的主方向 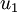 就是协方差矩阵
就是协方差矩阵 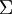 的主特征向量,而 变化的次方向
的主特征向量,而 变化的次方向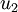 是次特征向量,以此类推。
是次特征向量,以此类推。
(证明略,事实上如果只是想实现算法这个定理不用理解。但我已决定重修线代(By Myself),因为越到后面越发现线性代数的重要性。)
3、我们可以通过matlab或其他线代软件求解出协方差矩阵的特征向量,并按列排列如下:
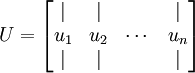
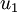 是主特征向量(对应最大的特征值),
是主特征向量(对应最大的特征值), 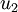 是次特征向量。以此类推,另记
是次特征向量。以此类推,另记 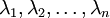 为相应的特征值(数值递减)。
为相应的特征值(数值递减)。
4、旋转数据。向量  构成了一个新基,可以用来表示数据。令
构成了一个新基,可以用来表示数据。令  为训练样本,那么
为训练样本,那么  就是样本点 i 在维度 上的投影的长度(幅值)。
就是样本点 i 在维度 上的投影的长度(幅值)。
至此,以二位空间为例,我们可以把  用
用 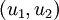 基表达为:
基表达为:
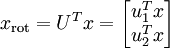
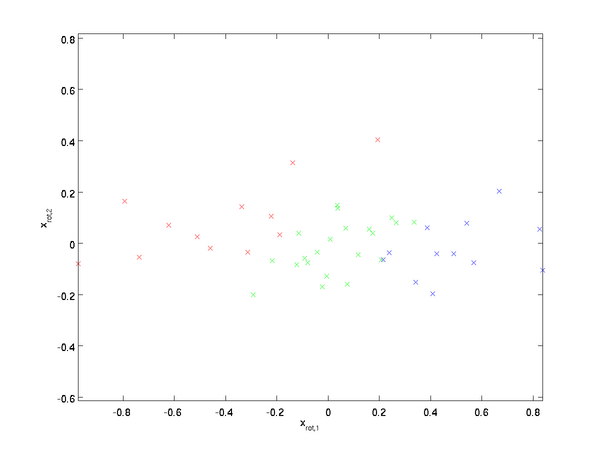
引用UFDL两张图
可见变化最大的维度(携带信息最多,在我们EE人的眼中,交流能量(方差)可以用来表征信号的信息)被排到了最前。
| 旋转前 | 旋转后 |
 |
 |
二、数据的取舍
接上,我们用方差来表征一个信号的信息,在旋转过后的数据中,我们把最后面方差较小的维度舍去。
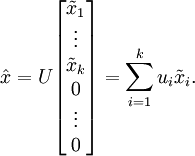
保留下来的数据与原数据所携带的信息比为
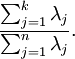
一般取
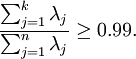
(若向他人介绍PCA算法详情,告诉他们你选择的  保留了99%的方差)
保留了99%的方差)
总的来说,PCA后,数据的近似表示
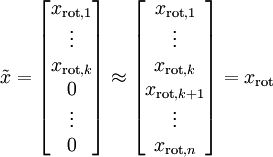
即,我们舍去n维向量中的(n-k)维,用k维向量来表示数据,可见数据的维度被缩小了。
如,舍去第二维之后的数据
三、复原
其实一般都不复原,那么辛苦排除了无用信息还复原干蛋。只是说有这么个东西……
矩阵 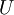 有正交性,即满足
有正交性,即满足 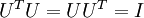 ,所以若想将旋转后的向量
,所以若想将旋转后的向量 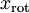 还原为原始数据
还原为原始数据  ,将其左乘矩阵
,将其左乘矩阵 即可:
即可: 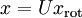 , 验算一下:
, 验算一下: 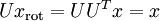 ,即:
,即:

白化(Whitening):
主要思想(教程上的):
由于图像中相邻像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性;更正式的说,我们希望通过白化过程使得学习算法的输入具有如下性质:(i)特征之间相关性较低;(ii)所有特征具有相同的方差。
方法:
在上一步PCA中,旋转过后的维度间已经不具有相关性(果真正交化?)。因此这里只用将数据的方差化为一即可。
可知协方差矩阵对角元素的值为 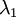 ,
,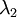 ……为数据方差,方差归一:
……为数据方差,方差归一:
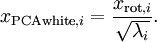
(对,就这么就完了,当然这只是最最最简单的东西)
TIPS:
未防止 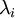 过于接近零,这样在缩放步骤时我们除以
过于接近零,这样在缩放步骤时我们除以 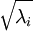 将导致除以一个接近0的值;这可能使数据上溢 。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数
将导致除以一个接近0的值;这可能使数据上溢 。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数 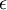 :
:
当  在区间
在区间 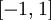 上时, 一般取值为
上时, 一般取值为 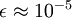 。
。
(教程上是这么说的,但是事实上我认为如果某一维度的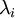 过于接近零,这个维度在PCA过程中将会被舍弃。可能教程中针对的是未经过PCA的数据即:ZCAWhite?)
过于接近零,这个维度在PCA过程中将会被舍弃。可能教程中针对的是未经过PCA的数据即:ZCAWhite?)
完结:?
基本上把几个月的深度学习自己过了一遍(虽然有相当一部分是复制粘贴的0)。
后面的池化和卷积就不写了,能用到的不多。
至于稀疏编码写不写,还要看学不学。
因为在UFLDL里面这方面的内容还未完善,
而且稀疏编码的激活函数都是可学习的,
不仅理解难度大,实现起来难度也大。
师兄学习的时候跑了两天………………何况我的I3-M一代。
暂且就这样吧。
接下来想学习python和theano,
提高应用能力,
然后向自己找点资料搞实验。(事实上已经找到)
不过需要指导老师,和老师打交道什么的最不懂了。
自学DL后深深感到线性代数知识的匮乏,需要恶补。
同时发现这个是DL因为可并行计算很多,很有硬件加速的前途(FPGA?不过矩阵运算好像还不成熟?)。
要是做成芯片肯定很有前途啊~
管他呢!
Deep Learning 学习笔记(9):主成分分析( PCA )与 白化( whitening )的更多相关文章
- 【deep learning学习笔记】注释yusugomori的DA代码 --- dA.h
DA就是“Denoising Autoencoders”的缩写.继续给yusugomori做注释,边注释边学习.看了一些DA的材料,基本上都在前面“转载”了.学习中间总有个疑问:DA和RBM到底啥区别 ...
- [置顶]
Deep Learning 学习笔记
一.文章来由 好久没写原创博客了,一直处于学习新知识的阶段.来新加坡也有一个星期,搞定签证.入学等杂事之后,今天上午与导师确定了接下来的研究任务,我平时基本也是把博客当作联机版的云笔记~~如果有写的不 ...
- Deep Learning 学习笔记(8):自编码器( Autoencoders )
之前的笔记,算不上是 Deep Learning, 只是为理解Deep Learning 而需要学习的基础知识, 从下面开始,我会把我学习UFDL的笔记写出来 #主要是给自己用的,所以其他人不一定看得 ...
- 深度学习入门教程UFLDL学习实验笔记三:主成分分析PCA与白化whitening
主成分分析与白化是在做深度学习训练时最常见的两种预处理的方法,主成分分析是一种我们用的很多的降维的一种手段,通过PCA降维,我们能够有效的降低数据的维度,加快运算速度.而白化就是为了使得每个特征能有同 ...
- 【deep learning学习笔记】Recommending music on Spotify with deep learning
主要内容: Spotify是个类似酷我音乐的音乐站点.做个性化音乐推荐和音乐消费.作者利用deep learning结合协同过滤来做音乐推荐. 详细内容: 1. 协同过滤 基本原理:某两个用户听的歌曲 ...
- 【deep learning学习笔记】注释yusugomori的RBM代码 --- 头文件
百度了半天yusugomori,也不知道他是谁.不过这位老兄写了deep learning的代码,包括RBM.逻辑回归.DBN.autoencoder等,实现语言包括c.c++.java.python ...
- Neural Networks and Deep Learning学习笔记ch1 - 神经网络
近期開始看一些深度学习的资料.想学习一下深度学习的基础知识.找到了一个比較好的tutorial,Neural Networks and Deep Learning,认真看完了之后觉得收获还是非常多的. ...
- paper 149:Deep Learning 学习笔记(一)
1. 直接上手篇 台湾李宏毅教授写的,<1天搞懂深度学习> slideshare的链接: http://www.slideshare.net/tw_dsconf/ss-62245351? ...
- Deep Learning 学习笔记——第9章
总览: 本章所讲的知识点包括>>>> 1.描述卷积操作 2.解释使用卷积的原因 3.描述pooling操作 4.卷积在实践应用中的变化形式 5.卷积如何适应输入数据 6.CNN ...
随机推荐
- 敏捷BI与数据驱动机制
大数据这件事,整体上还是说的多一些,做的稍微少一点.大数据可以是荒凉高原上波澜壮阔的机房,也可以润物细无声般融入到日常生活和工作.换句话说,大数据应该是一种文化. 在个人层面,很多人对数字和计算并不敏 ...
- TeamTalk源码分析(十一) —— pc客户端源码分析
--写在前面的话 在要不要写这篇文章的纠结中挣扎了好久,就我个人而已,我接触windows编程,已经六七个年头了,尤其是在我读研的三年内,基本心思都是花在学习和研究windows程序上 ...
- hdu 1098
http://acm.hdu.edu.cn/showproblem.php?pid=1098 假设x=m时,65|f(m),即65|5*m^13+13*m^5+k*a*m 计算f(m+1)=(5*m^ ...
- IOS开发 CocoaPods 使用 pod Install 出现 Updating local specs repositories
pod install 换成pod install --verbose --no-repo-update这个命令,前面的命令被墙了
- ICE实现服务器客户端
本文将结合实际项目,做一个基于ice的实际项目实例应用,该实例完成客户端调用服务端接口完成消息发送,计算的功能.1,创建java项目ICEServer,导入ice.jar. 2,在项目下创建slice ...
- 程序设计入门-C语言基础知识-翁恺-第七周:指针与字符串-详细笔记(七)
目录 第七周:指针与字符串 7.1 指针初步 7.2 字符类型 7.3 字符串 7.3 课后练习 第七周:指针与字符串 7.1 指针初步 sizeof 是一个运算符,给出某个类型或变量在内存中所占据的 ...
- C的动态链表建立
运用到的函数为: 动态内存分配函数malloc() 比如:char *name=(char *)malloc(20); 相当与c++的new关键字 动态内存释放函数free ...
- HDU1520 Anniversary party 树形DP基础
There is going to be a party to celebrate the 80-th Anniversary of the Ural State University. The Un ...
- tensorflow图像基本处理
tensorflow库提供的专门的图片处理库,以下只是部分示例,更多函数请参照源码'\tensorflow_api\v1\image__init__.py' 加载图像 方式1: 使用tf.gfile. ...
- test20181223
Written with StackEdit. T1 取石子(stone) Description 有\(n\)堆石子,第\(i\)堆有\(x_i\)个. \(Alice\)和\(Bob\)轮流取石子 ...