[GYM 100492A] Average Convex Hull 凸包好题

大致题意：

　　给出一个点集，其中有一个点有相同的几率会被删除，求删除之后的点集够成的凸包上的点的平均数。

　　

　　　　　　　　首先看到题目，可以考虑枚举删除的点，将其凸包上前后两点以及两点间凸包内所有点构建凸包，因为凸包内每个点

　　　　　　最多被访问一次，所以是O(N)的复杂度。理论上可行，但是实际上实现起来相当困难，又兴趣的可以去尝试。

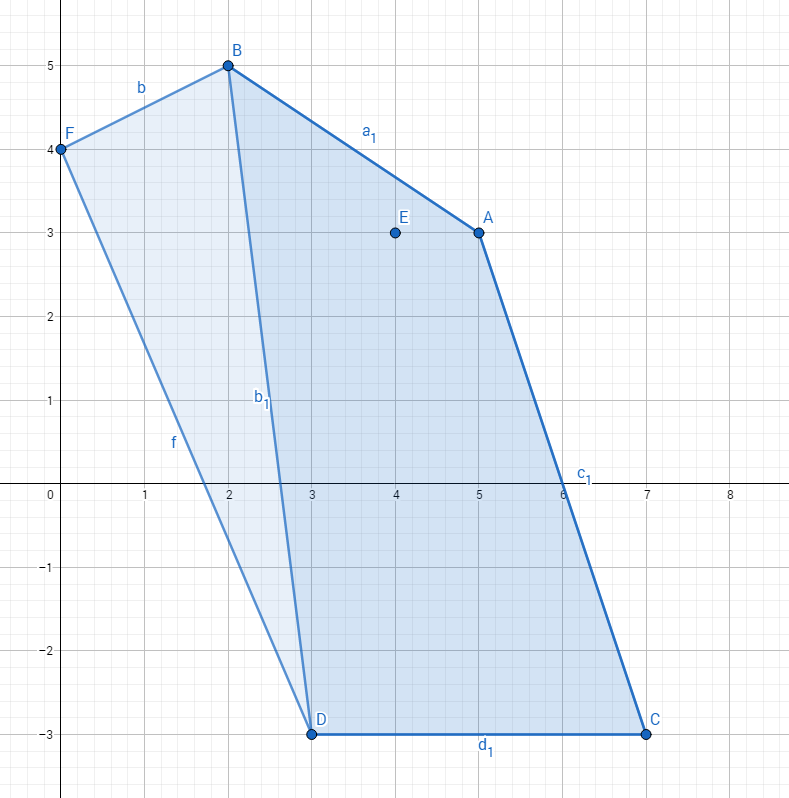
　　　　　　　　这题的正解是先将所有的点求个凸包，若凸包顶点为偶数，则只需先删除凸包上的所有奇数点，然后求得一个凸包，然

　　　　　　后再删除凸包上偶数点，在求一次凸包，最后答案为

　　　　　　　　　　　　ans=两个凸包的顶点数+（m-1）*m-构建前两个凸包时经过的凸包的点数+删除的点在凸包内部的情况

　　　　　　奇数点同理，但要多计算一次。

　　　　　　附图  偶数点时

　　　　　　　

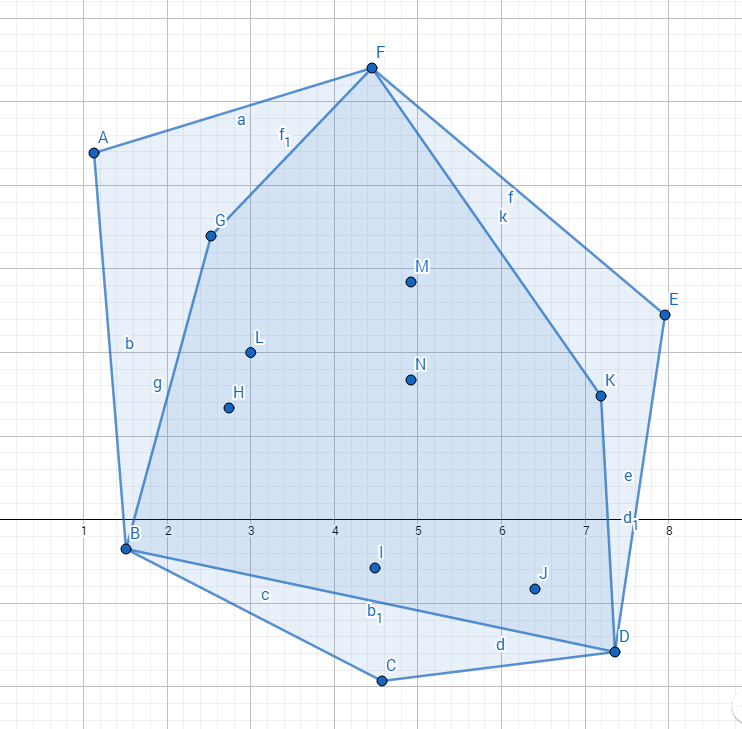
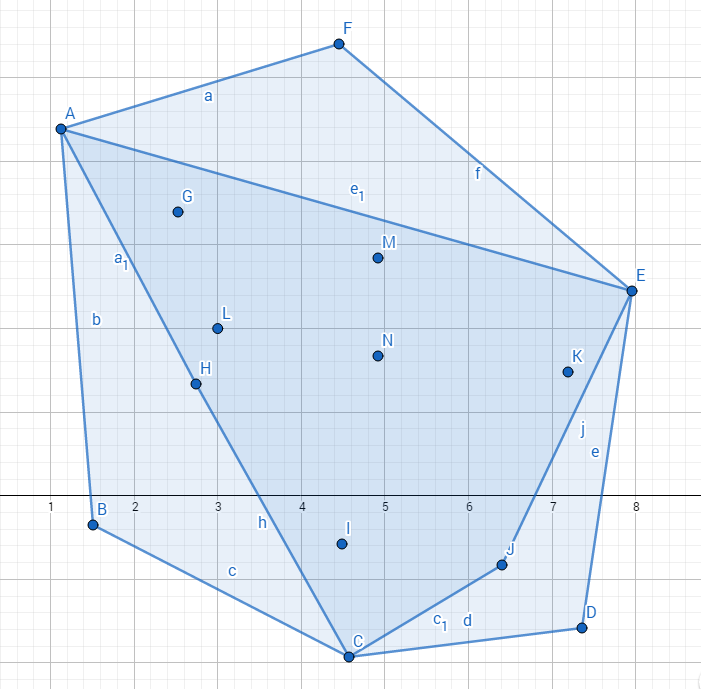
　　　　　　奇数点时

　　

　　　　

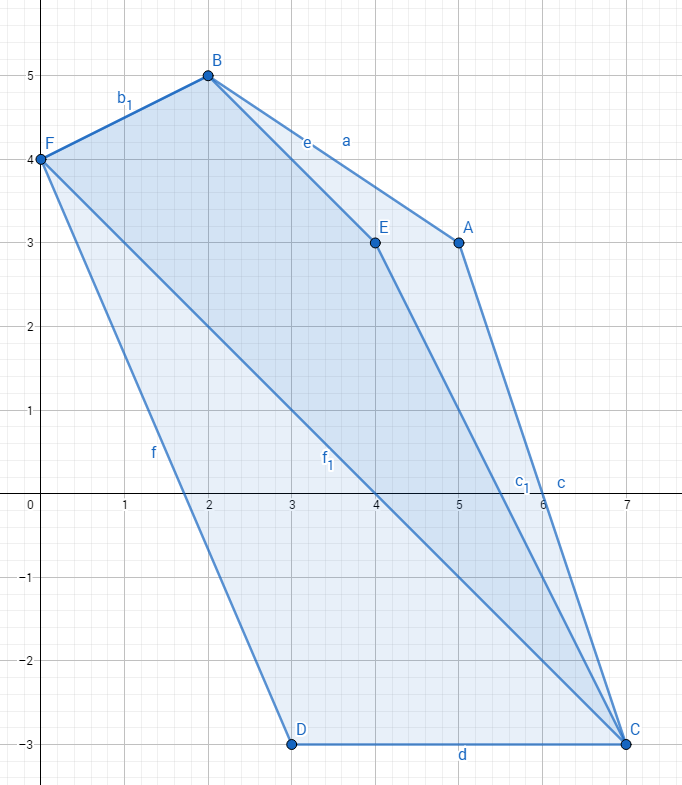
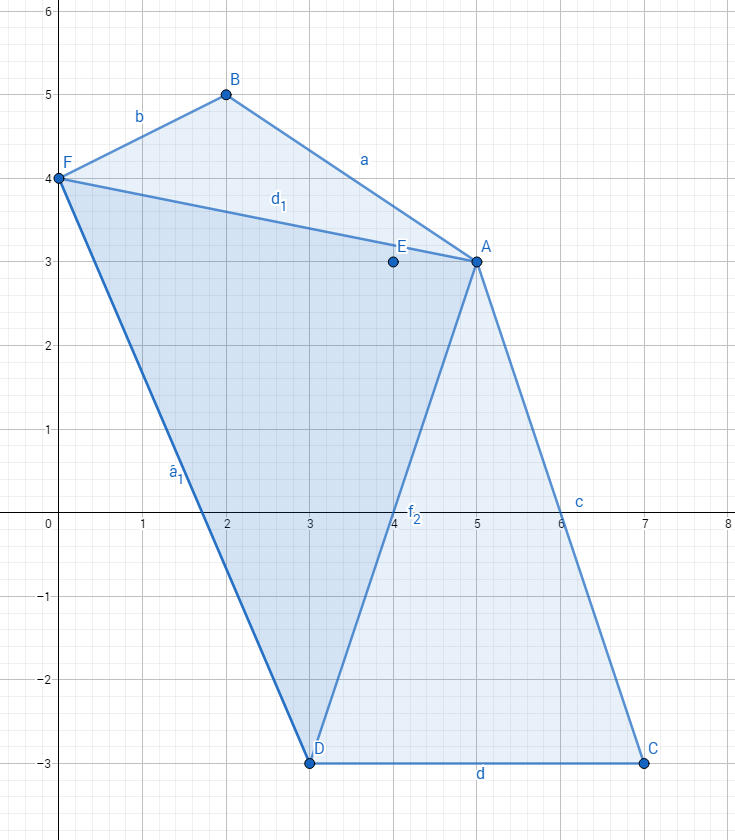
 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<algorithm>
 #include<queue>
 #include<set>
 #include<map>
 #include<stack>
 #include<time.h>
 #include<cstdlib>
 #include<cmath>
 #include<list>
 using namespace std;
 #define MAXN 200100
 #define eps 1e-5
 #define For(i,a,b) for(int i=a;i<=b;i++)
 #define Fore(i,a,b) for(int i=a;i>=b;i--)
 #define lson l,mid,rt<<1
 #define rson mid+1,r,rt<<1|1
 #define mkp make_pair
 #define pb push_back
 #define cr clear()
 #define sz size()
 #define met(a,b) memset(a,b,sizeof(a))
 #define iossy ios::sync_with_stdio(false)
 #define fre freopen
 #define pi acos(-1.0)
 #define inf 1e9+9
 #define Vector Point
 const int Mod=1e9+;
 typedef unsigned long long ull;
 typedef long long ll;
 typedef pair<int,int> pii;
 typedef pair<ll,ll> pll;
 int dcmp(double x){
     if(fabs(x)<=eps) return ;
     return x<?-:;
 }
 struct Point {
     double x,y;
     int id;
     int pre,nxt;
     Point(double x=,double y=) : x(x),y(y) {}
     Point operator - (const Point &a)const{ return Point(x-a.x,y-a.y); }
     Point operator + (const Point &a)const{ return Point(x+a.x,y+a.y); }
     Point operator * (const double &a)const{ return Point(x*a,y*a); }
     Point operator / (const double &a)const{ return Point(x/a,y/a); }
     bool operator < (const Point &a)const{    if(x==a.x) return y<a.y;return x<a.x; }
     bool operator == (const Point &a)const{ return dcmp(x-a.x)== && dcmp(y-a.y)==; }
     void read(int iid=) { scanf("%lf%lf",&x,&y);id=iid; }
     void out(){cout<<"Bug: "<<x<<" "<<y<<endl;}
 };
 inline double Cross(Vector a,Vector b) { return a.x*b.y-a.y*b.x; }
 inline double Dot(Vector a,Vector b) { return a.x*b.x+a.y*b.y; }
 inline double dis(Vector a) { return sqrt(Dot(a,a)); }
 int ConvexHull(Point *p,int n,Point *ch){
     int m=;
     sort(p,p+n);
     For(i,,n-){
         p[i].id=i;
         while(m> && Cross(ch[m-]-ch[m-],p[i]-ch[m-])<=) m--;
         ch[m++]=p[i];
     }
     int k=m;
     Fore(i,n-,){
         while(m>k && Cross(ch[m-]-ch[m-],p[i]-ch[m-])<=) m--;
         ch[m++]=p[i];
     }
     if(n>) m--;
     return m;
 }
 inline bool Onsegment(Point a,Point b1,Point b2){
     return dcmp(Cross(b1-a,b2-a))== && dcmp(Dot(b1-a,b2-a))<;
 }
 bool Intersect_Segm_Segm(Point a1,Point a2,Point b1,Point b2){
     if(a1==b1 || a1==b2 || a2==b1 || a2==b2) return ;
     if(Onsegment(a1,b1,b2) || Onsegment(a2,b1,b2)) return ;
     double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1);
     double c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1);
     return dcmp(c1)*dcmp(c2)< && dcmp(c3)*dcmp(c4)<;
 }
 Point Intersect_Line_Point(Point p,Vector u,Point q,Vector v){
     Vector w=p-q;
     double t=Cross(v,w)/Cross(u,v);
     return p+u*t;
 }
 int vis[MAXN],vvis[MAXN];
 int tcnt;
 int tConvexHull(Point *p,int n,Point *ch){
     int m=;
     sort(p,p+n);
     For(i,,n-){
         if(vis[p[i].id]) continue;
         while(m> && Cross(ch[m-]-ch[m-],p[i]-ch[m-])<=) m--;
         ch[m++]=p[i];
     }
     int k=m;
     Fore(i,n-,){
         if(vis[p[i].id]) continue;
         while(m>k && Cross(ch[m-]-ch[m-],p[i]-ch[m-])<=) m--;
         ch[m++]=p[i];
     }
     if(ch[]==ch[m-]) m--;
     For(i,,m-){
         if(vvis[ch[i].id]) tcnt++;
     }
     return m;
 }
 ll n;
 Point ch[MAXN],p[MAXN],stk[MAXN];
 int solve(){
     scanf("%lld",&n);
     tcnt=;
     met(vis,);
     met(vvis,);
     For(i,,n-) p[i].read(i);
     int m=ConvexHull(p,n,ch);
     For(i,,m-) vvis[ch[i].id]=;
     if(n==) return puts("0/1");
     ll ans=m*1LL*(n-m);
     if(m%==){
         For(i,,m-){
             vis[ch[i].id]=;
             i++;
         }
         ans+=tConvexHull(p,n,stk);
         met(vis,);
         For(i,,m-){
             vis[ch[i].id]=;
             i++;
         }
         ans+=tConvexHull(p,n,stk);
     }else{
         For(i,,m-){
             vis[ch[i].id]=;
             i++;
         }
         ans+=tConvexHull(p,n,stk);
         met(vis,);
         For(i,,m-){
             vis[ch[i].id]=;
             i++;
         }
         ans+=tConvexHull(p,n,stk);
         met(vis,);
         vis[ch[].id]=;
         ans+=tConvexHull(p,n,stk);
     }
     ans+=m*1LL*(m-)-tcnt;
     ll cnt=__gcd(ans,n);
     ans/=cnt;
     n/=cnt;
     printf("%lld/%lld\n",ans,n);
 }
 int main(){
 //  fre("in.txt","r",stdin);
     fre("average.in","r",stdin);
     fre("average.out","w",stdout);
     int t=;
     solve();
     return ;
 }