3298: [USACO 2011Open]cow checkers

Time Limit: 10 Sec Memory Limit: 128 MB
Submit: 65 Solved: 26
[Submit][Status][Discuss]

Description

　　　一天，Besssie准备和FJ挑战奶牛跳棋游戏。这个游戏上在一个M*N（1<=M<=1,000,000;1<=N<=1,000,000）的棋盘上，
这个棋盘上在（x,y）(0<=x棋盘的左下角是（0，0）坐标，棋盘的右上角是坐标（M-1,N-1）。
Bessie每次都是第一个移动棋子，然后Bessie与Fj轮流移动。每一轮可以做以下三种中的一种操作：
1）在同一行，将棋子从当前位置向左移动任意格；
2）在同一列，将棋子从当前位置向下移动任意格；
3）将棋子从当前位置向下移动k格再向左移动k格（k为正整数，且要满足移动后的棋子仍然在棋盘上）

第一个不能在棋盘上移动的人比赛算输（因为棋子处在（0,0）点）。
共有T个回合（1<=T<=1,000）,每次给出一个新起始点的坐标（x,y）,确定是谁赢。

Input

第1行：两个用空格隔开的整数M和N；
第2行：一个整数T；
第3到第T+2行：两个用空格隔开的整数x和y.

Output

第1到T行：包含“Farmer John”或者是“Bessie”，表示谁赢了这轮游戏。

Sample Input

3 3
1
1 1

Sample Output

Bessie

HINT

Source

Silver

题解：实际上，一上来此题目不难想到可以通过DP（或者记忆化搜索也行）来搞，但这样问题来了——N,M<=1000000，显然会爆。。。

于是只好来另辟蹊径——（明确两个概念：死点：表示当某一方在还未走这一步之前如果落到了这个位置将必死无疑的点活点：正好相反）

1.题目中说从(N-1,M-1)走到(0,0)，既然这样，我们何不看作从(0,0)走到(N-1,M-1)呢？

2.题目中说可以横向走，可以纵向走，可以斜向走，这不就意味着只要某一点被认定为死点，则这一个点横向、纵向、斜向上的其他点都是活点么（很明显如果某人走到了死点横向、斜向、纵向上的其他点上的话，他就可以把对手一步送到死点上，结束战斗。。。）

3.由2可知，所有的死点必然不在同一行，同一列，同一对角线上，也就是说对于某一x或者y坐标而言，其上死点的坐标是唯一的

4.所以综上所述，可以通过简单的O(N)预处理来实现求出每一个x坐标上的死点位置，然后接下来对于每个询问只要O(1)判断是否相同即可

于是，我们来开始找规律：

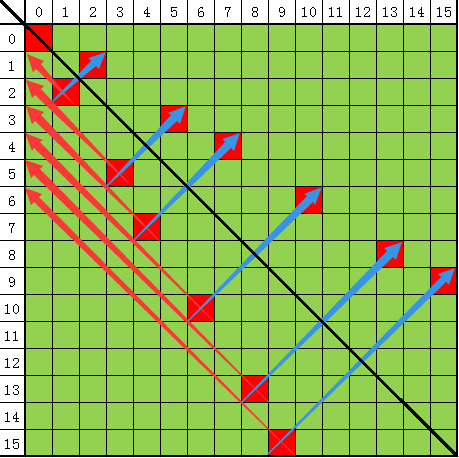
如上图，黑色的斜线表示对称轴，蓝箭头连着的是对称的，而红色箭头均为与对称轴平行的线，很明显所有下半边的点所在的线间隔都是1单位，这样一来规律就很分明了——对于当前的x坐标，要么已经通过之前的某点对称得到了结果，如果没得到的话，那就根据上一个同侧的点从斜线方向挪一格，然后对称一下得出上半边那个点，实现快速求解

 /**************************************************************

     Problem:

     User: HansBug

     Language: Pascal

     Result: Accepted

     Time: ms

     Memory: kb

 ****************************************************************/

 var

    i,j,k,l,m,n:longint;

    a:array[..] of longint;

 function max(x,y:longint):longint;

          begin if x>y then max:=x else max:=y; end;

 begin

      fillchar(a,sizeof(a),-);

      a[]:=;l:=; readln(n,m);

      for i:= to max(m,n) do

          begin if a[i]>- then continue;

          inc(l);a[i]:=i+l;if (i+l)<= then a[i+l]:=i; end;

      readln(n);

      for i:= to n do

          begin

               readln(j,k);

               if k>j then begin l:=k;k:=j;j:=l end;

               if a[j]<>k then writeln('Bessie') else writeln('Farmer John');

          end;

 end.