Kruskal算法的简单实现

嘛嘛嘛，好像大家在实现Kruskal算法是都是用的边集数组，判断图的连通性咱不会,o(╯□╰)o（并查集诶）。

Kruskal算法：

规则：

（1）对每一条边按照从小到大进行排序。

（2）加入边的时候判断这条边与之前的边是否构成回路，如果构成则放弃这条边，否则就加入到最小生成树中。

边集数组：

struct Edge{
    int begin;
    int end;
    int weight;
};

起点，终点，权值，这些都好懂的。

然后判断是否构成回路则是采用了并查集的思想：大家如果不懂并查集，可以看看这篇博客:并查集详解这篇博文,当初就是看这篇博文入门的。

整个代码:

#include <algorithm>
#include <iostream>
using namespace std;
const int MAXSIZE=;

struct node{
      int begin;
      int end;
      int weight;
    }Gnode[MAXSIZE];

int parent[MAXSIZE];

int Parent(int f){
    while(parent[f]!=f){
    f=parent[f];
    }
  return f;
}
int cmp(node s1,node s2){
    return s1.weight<s2.weight;
}
void Kruskal(node p[],int k){
  int n,m;
  for(int i=;i<=MAXSIZE;i++){
   parent[i]=i;
  }
  sort(p,p+k,cmp);
  for(int i=;i<=k;i++){
  n=Parent(p[i].begin);
  m=Parent(p[i].end);
  if(n!=m){
  cout<<'V'<<p[i].begin<<" "<<'V'<<p[i].end<<" "<<p[i].weight<<endl;
  parent[n]=m;
  }
  }
}
int main(){
    cout<<"Kruskal算法求最小生成树"<<endl;
    cout<<"请输入图的边数"<<endl;
    int num;
    cin>>num;
    for(int i=;i<=num;i++){
       cin>>Gnode[i].begin>>Gnode[i].end>>Gnode[i].weight;
    }
    cout<<"最小生成树的每条边级其权值"<<endl;
    Kruskal(Gnode,num);
    return ;
}

附上测试数据：

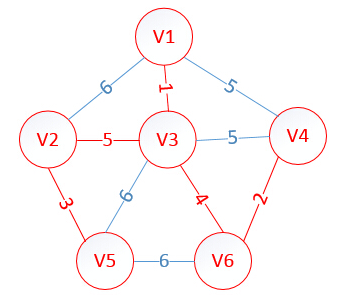
这是最后构建出的最小生成树。

并查集的思想很简单：首先判断两个点的父亲节点是否相同，不相同则让其中一个父亲节点成为另一个父亲节点的子节点，这样大家都在一个集合里了，如果最后加入的边首位节点都在一个集合里，显然这就构成回路了。

以上图为例：        1   3     parent[1]=1     parent[3]=3   则parent[1]=3    parent[3]=3

4   6     parent[4]=4     parent[6]=6   则parent[4]=6    parent[6]=6

2   5     parent[2]=2     parent[5]=5   则parent[2]=5    parent[5]=5

3   6     parent[3]=3     parent[6]=6   则parent[3]=6    parent[6]=6

2   3     parent[2]=5     parent[3]=6   则parent[5]=6    parent[3]=6

2   1     parent[2]=6     parent[1]=6   这样构成了回路

还有一点要强调的是上面代码中parent函数没有路径压缩这一过程，数据量比较大时，可能会超时，当然大家采用递归写法的话就不用考虑这个问题了。

int Parent(int f){
    if(parent[f]!=f)
       parent[f]=Parent(parent[f]);
    return parent[f];
}