生成学习算法(Generative Learning algorithms)
一、引言
前面我们谈论到的算法都是在给定\(x\)的情况下直接对\(p(y|x;\theta)\)进行建模。例如,逻辑回归利用\(h_\theta(x)=g(\theta^T x)\)对\(p(y|x;\theta)\)建模,这类算法称作判别学习算法。
考虑这样一个分类问题,我们根据一些特征来区别动物是大象\((y=1)\)还是狗\((y=0)\)。给定了这样一个训练集,逻辑回归或感知算法要做的就是去找到一个决策边界,将大象和狗的样本分开来。可以换个思路,首先根据大象的特征来学习出一个大象的模型,然后根据狗的特征学习出狗的模型,对于一个新的样本,提取它的特征先放到大象的模型中求得是大象的概率,然后放到狗的模型中求得是狗的概率,最后我们比较两个概率哪个大,即确定这个动物是哪种类型。也即求\(p(y|x)=\frac{p(x|y)p(y)}{p(x)}\),\(y\)为输出结果,\(x\)为特征。
现在我们来定义这两种解决问题的方法:
判别学习算法(discriminative learning algorithm):直接学习\(p(y|x)\)或者是从输入直接映射到输出的方法
生成学习算法(generative learning algorithm):对\(p(x|y)\)(也包括\(p(y))\)进行建模。
\(y\)为输出变量,值为0或1,如果是大象取1,狗则取0
\(p(x|y = 0)\):对狗的特征进行建模
\(p(x|y = 1)\):对大象的特征建模
对\(p(x|y)\)和\(p(y)\)完成建模后,运用贝叶斯公式,就可以求得在给定\(x\)的情况下\(y\)的概率:
\[p(y|x)=\frac{p(x|y)p(y)}{p(x)}\]
\[p(x) = p(x|y = 1)p(y = 1) + p(x|y =0)p(y = 0)\]
由于我们关心的是\(y\)离散结果中哪一个的概率更大,而不是要求得具体的概率,所以上面的公式我们可以表达为:
\begin{align*} arg\,\underset{y}{max}p(y|x) &=arg\,\underset{y}{max}\frac{p(x|y)p(y)}{p(x)} \\
&=arg\,\underset{y}{max}p(x|y)p(y) \end{align*}
\(arg\,\underset{y}{max}p(y|x)\)的含义:满足条件的最大\(y\)值。对\(y\)求取最大值,与\(p(x)\)无关,所以可以不需要计算\(p(x)\)了
常见的生成模型有:隐马尔可夫模型HMM、朴素贝叶斯模型、高斯混合模型GMM、LDA等
二、高斯判别分析(Gaussian Discriminant Analysis)
下面介绍第一个生成学习算法GDA。在GDA中,假设\(x \in R^n\)且是连续的,且\(p(x|y)\)满足多项正态分布。
2.1 多项正态分布(The multivariate normal distribution)
假设随机变量\(X\)满足\(n\)维的多项正态分布,参数为均值向量\(\mu\in R^n\),协方差矩阵\(\Sigma \in R^{n\times n}\),记为\(N(\mu,\Sigma)\)其概率密度表示为:
\[p(x;\mu,\Sigma)=\frac{1}{(2\pi)^{n/2}(det\Sigma)^\frac{1}{2}}exp\bigg(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\bigg)\]
\(det\Sigma\)表示矩阵\(\Sigma\)的行列式(determinant)。
均值向量 :\(\mu\)
协方差矩阵:\(\Sigma=E[(X-E[X])(X-E[X])^T]=E[(x-\mu)(x-\mu)^T]\)
接下来我们用matlab来画一下二维正态分布的图像,我们可以调整均值和协方差矩阵来观察图像。
代码:
mu=[0 0];
sigma=[1.0 0;0 1.0];
[x y]=meshgrid(linspace(-3,3,40)',linspace(-3,3,40)');
X=[x(:) y(:)];
z=mvnpdf(X,mu,sigma);
surf(x,y,reshape(z,40,40));
hold on;
figure;
contour(x,y,reshape(z,40,40));
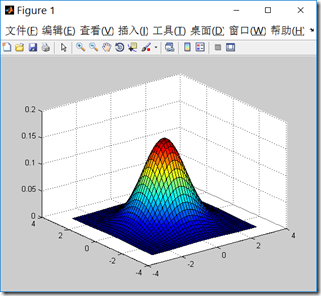
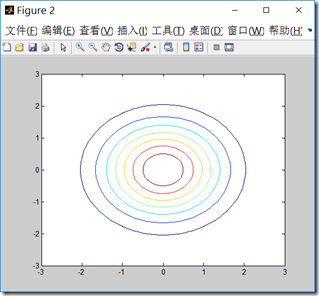
\(\mu\)决定中心位置,\(\Sigma\)决定投影椭圆的朝向和大小。
2.2高斯判别分析模型(The Gaussian Discriminant Analysis model)
现在有一个分类问题,训练集的特征值\(x\)是随机连续值,那么我们可以利用高斯判别分析模型,假设\(p(x|y)\)满足多值正态分布,即:
\[y \sim Bernoulli(\phi)\]
\[x|y=0 \sim N(\mu_0, \Sigma)\]
\[x|y=1 \sim N(\mu_1, \Sigma)\]
概率分布为:
\[p(y) = \phi^y(1-\phi)^{1-y}\]
\[p(x|y=0) = \frac{1}{(2\pi)^{n/2}(det\Sigma)^\frac{1}{2}}exp\bigg(-\frac{1}{2}(x-\mu_0)^T\Sigma^{-1}(x-\mu_0)\bigg)\]
\[p(x|y=1) = \frac{1}{(2\pi)^{n/2}(det\Sigma)^\frac{1}{2}}exp\bigg(-\frac{1}{2}(x-\mu_1)^T\Sigma^{-1}(x-\mu_1)\bigg)\]
模型参数为\(\phi, \Sigma, \mu_0, \mu_1\),对数似然函数为:
\[l(\phi,\mu_0,\mu_1,\Sigma)=log\prod_{i=1}^{m}p(x^{(i)},y^{(i)};\phi,\mu_0,\mu_1,\Sigma)=log\prod_{i=1}^{m}p(x^{(i)}|y^{(i)};\mu_0,\mu_1,\Sigma)p(y^{(i)};\phi)\]
注意这里的参数有两个\(\mu\),表示在不同的结果模型下,特征均值不同,但我们假设协方差相同。反映在图上就是不同模型中心位置不同,但形状相同。这样就可以用直线来进行分隔判别。
求得所有的参数:
\[\phi = \frac{1}{m}\sum\limits_{i=1}^{m}1\{y^{(i)}=1\}\]
\[\mu_0=\frac{\sum\limits_{i=1}^{m}1\{y^{(i)}=0\}x^{(i)}}{\sum\limits_{i=1}^{m}1\{y^{(i)}=0\}}\]
\[\mu_1=\frac{\sum\limits_{i=1}^{m}1\{y^{(i)}=1\}x^{(i)}}{\sum\limits_{i=1}^{m}1\{y^{(i)}=1\}}\]
\[\Sigma = \frac{1}{m}\sum\limits_{i=1}^{m}(x^{(i)}-\mu_{y{(i)}})(x^{(i)}-\mu_{y{(i)}})^T\]
\(\phi\)是训练样本中结果\(y=1\)占有的比例。
\(\mu_0\)是\(y=0\)的样本中特征均值。
\(\mu_1\)是\(y=1\)的样本中特征均值。
\(\Sigma\)是样本特征方差均值。
所以通过上面所述,画出图像如下图:
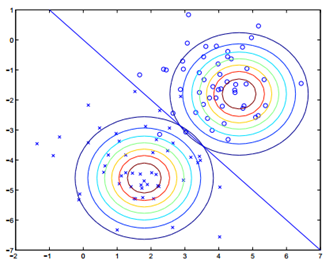
直线两边的\(y\)值不同,但协方差矩阵相同,因此形状相同,\(\mu\)不同,因此位置不同。
2.3讨论GDA和逻辑回归(Discussion: GDA and logistic regression)
现在我们把\(p(y = 1|x; \phi, \mu_0, \mu_1, \Sigma)\)看成是\(x\)的函数,则可以表达为:
\[p(y=1|x;\phi,\Sigma,\mu_0,\mu_1)=\frac{1}{1+exp(-\theta^Tx)}\]
\(\theta\) 是参数\(\phi,\Sigma,\mu_0,\mu_1\)的函数,这正是逻辑回归的形式。
逻辑回归和GDA在训练相同的数据集的时候我们得到两种不同的决策边界,那么怎么样来进行选择模型呢:
上面提到如果\(p(x|y)\)是一个多维的高斯分布,那么\(p(y|x)\)可以推出一个logistic函数;反之则不一定正确,\(p(y|x)\)是一个logistic函数并不能推出\(p(x|y)\)服从高斯分布.这说明GDA比logistic回归做了更强的模型假设.
如果\(p(x|y)\)真的服从或者趋近于服从高斯分布,则GDA比logistic回归效率高.
当训练样本很大时,严格意义上来说并没有比GDA更好的算法(不管预测的多么精确).
事实证明即使样本数量很小,GDA相对logisic都是一个更好的算法.
但是,logistic回归做了更弱的假设,相对于不正确的模型假设,具有更好的鲁棒性(robust).许多不同的假设能够推出logistic函数的形式. 比如说,如果\(x|y=0 \sim Poisson(\lambda_0)\),\(x|y=1 \sim Poisson(\lambda_1)\)那么\(p(y|x)\)是logistic。
logstic回归在这种类型的Poisson数据中性能很好. 但是如果我们使用GDA模型,把高斯分布应用于并不是高斯数据中,结果是不好预测的,GDA就不是很好了.
三:朴素贝叶斯(Naive Bayes)
在GDA中,特征向量\(x\)是连续的实数向量,那么现在谈论一下当\(x\)是离散时的情况。
我们沿用对垃圾邮件进行分类的例子,我们要区分邮件是不是垃圾邮件。分类邮件是文本分类的一种应用
将一封邮件作为输入特征向量,与现有的字典进行比较,如果在字典中第i个词在邮件中出现,则\(x_i=1\),否则\(x_i =0\),所以现在我们假设输入特征向量如下:
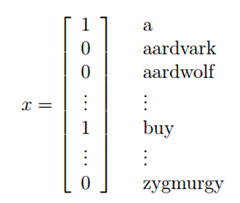
选定特征向量后,现在要对\(p(x|y)\)进行建模:
假设字典中有50000个词,\(x \in \{0, 1\}^{50000}\) 如果采用多项式建模, 将会有\(2^{50000}\)种结果,\(2^{50000}-1\)维的参数向量,这样明显参数过多。所以为了对\(p(x|y)\)建模,需要做一个强假设,假设\(x\)的特征是条件独立的,这个假设称为朴素贝叶斯假设(Naive Bayes (NB) assumption),这个算法就称为朴素贝叶斯分类(Naive Bayes classifier).
解释:
如果有一封垃圾邮件\((y=1)\),在邮件中出现buy这个词在2087这个位置,它对39831这个位置是否出现price这个词没有影响,也就是,我们可以这样表达\(p(x_{2087}|y)=p(x_{2087}|y,x_{39831})\),这个和\(x_{2087}\)和\(x_{39831}\)相互独立不同,如果相互独立,则可以写为\(p(x_{2087})=p(x_{2087}|x_{39831})\),我们这里假设的是在给定y的情下,\(x_{2087}\)和\(x_{39831}\)独立。
现在我们回到问题中,在做出假设后,可以得到:
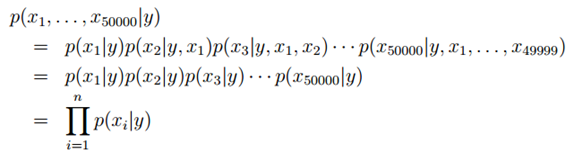
解释
第一个等号用到的是概率的性质 链式法则
第二个等式用到的是朴素贝叶斯假设
朴素贝叶斯假设是约束性很强的假设,一般情况下 buy和price是有关系的,这里我们假设的是条件独立 ,独立和条件独立不相同
模型参数:
\[\phi_{i|y=1}=p(x_i=1|y=1)\]
\[\phi_{i|y=0}=p(x_i=1|y=0)\]
\[\phi_y=p(y=1)\]
对于训练集{(x(i) , y(i)); i =1, . . . , m},根据生成学习模型规则,联合似然函数(joint likelihood)为:
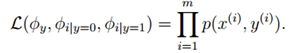
得到最大似然估计值:

最后一个式子是表示\(y=1\)的样本数占全部样本数的比例,前两个表示在\(y=1\)或\(y=0\)的样本中,特征\(x_j=1\)的比例。
拟合好所有的参数后,如果我们现在要对一个新的样本进行预测,特征为x,则有:
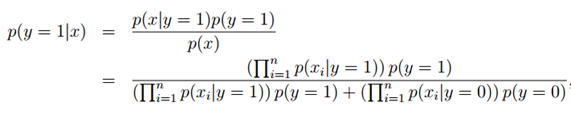
实际上只要比较分子就行了,分母对于y = 0和y = 1是一样的,这时只要比较p(y = 0|x)与p(y = 1|x)哪个大就可以确定邮件是否是垃圾邮件。
3.1拉普拉斯平滑(Laplace smoothing)
朴素贝叶斯模型可以在大部分情况下工作良好。但是该模型有一个缺点:对数据稀疏问题敏感。
比如在邮件分类中,对于低年级的研究生,NIPS显得太过于高大上,邮件中可能没有出现过,现在新来了一个邮件"NIPS call for papers",假设NIPS这个词在词典中的位置为35000,然而NIPS这个词从来没有在训练数据中出现过,这是第一次出现NIPS,于是算概率时:
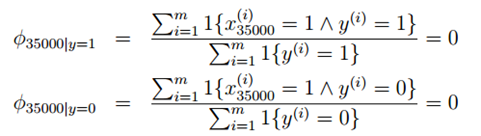
由于NIPS从未在垃圾邮件和正常邮件中出现过,所以结果只能是0了。于是最后的后验概率:

对于这样的情况,我们可以采用拉普拉斯平滑,对于未出现的特征,我们赋予一个小的值而不是0。具体平滑方法为:
假设离散随机变量取值为{1,2,···,k},原来的估计公式为:

使用拉普拉斯平滑后,新的估计公式为:
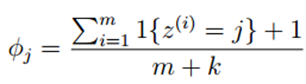
即每个k值出现次数加1,分母总的加k,类似于NLP中的平滑,具体参考宗成庆老师的《统计自然语言处理》一书。
对于上述的朴素贝叶斯模型,参数计算公式改为:
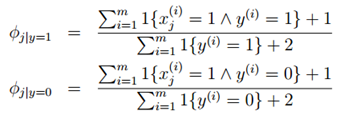
生成学习算法(Generative Learning algorithms)的更多相关文章
- 【cs229-Lecture5】生成学习算法:1)高斯判别分析(GDA);2)朴素贝叶斯(NB)
参考: cs229讲义 机器学习(一):生成学习算法Generative Learning algorithms:http://www.cnblogs.com/zjgtan/archive/2013/ ...
- Andrew Ng机器学习公开课笔记 -- Generative Learning algorithms
网易公开课,第5课 notes,http://cs229.stanford.edu/notes/cs229-notes2.pdf 学习算法有两种,一种是前面一直看到的,直接对p(y|x; θ)进行建模 ...
- CS229笔记:生成学习算法
在线性回归.逻辑回归.softmax回归中,学习的结果是\(p(y|x;\theta)\),也就是给定\(x\)的条件下,\(y\)的条件概率分布,给定一个新的输入\(x\),我们求出不同输出的概率, ...
- [置顶] 生成学习算法、高斯判别分析、朴素贝叶斯、Laplace平滑——斯坦福ML公开课笔记5
转载请注明:http://blog.csdn.net/xinzhangyanxiang/article/details/9285001 该系列笔记1-5pdf下载请猛击这里. 本篇博客为斯坦福ML公开 ...
- Stanford大学机器学习公开课(五):生成学习算法、高斯判别、朴素贝叶斯
(一)生成学习算法 在线性回归和Logistic回归这种类型的学习算法中我们探讨的模型都是p(y|x;θ),即给定x的情况探讨y的条件概率分布.如二分类问题,不管是感知器算法还是逻辑回归算法,都是在解 ...
- CS229 Lesson 5 生成学习算法
课程视频地址:http://open.163.com/special/opencourse/machinelearning.html 课程主页:http://cs229.stanford.edu/ 更 ...
- Generative Learning algorithms
"generative algorithm models how the data was generated in order to categorize a signal. It ask ...
- Machine Learning Algorithms Study Notes(2)--Supervised Learning
Machine Learning Algorithms Study Notes 高雪松 @雪松Cedro Microsoft MVP 本系列文章是Andrew Ng 在斯坦福的机器学习课程 CS 22 ...
- Machine Learning Algorithms Study Notes(1)--Introduction
Machine Learning Algorithms Study Notes 高雪松 @雪松Cedro Microsoft MVP 目 录 1 Introduction 1 1.1 ...
随机推荐
- C#并行编程(6):线程同步面面观
理解线程同步 线程的数据访问 在并行(多线程)环境中,不可避免地会存在多个线程同时访问某个数据的情况.多个线程对共享数据的访问有下面3种情形: 多个线程同时读取数据: 单个线程更新数据,此时其他线程读 ...
- 初识thinkphp(4)
这次内容是数据库的使用方法 因为在第一章讲过就是拿index这个文件写的数据库的访问,这次实验我使用文件是系统默认的首页 配置的内容也在那里有提过就不重发戳图了. 数据库按照手册上的建议建了3行的内容 ...
- 概率dp总结
终于做到概率dp题了,开个总结帖记录一下 首先是几篇论文:有关概率和期望问题的研究 做了这么多题,实际上没什么特别好总结的,就是搞清状态和转移,顺着写就行了,和基本dp差不多 概率是由过去到现在dp[ ...
- Codeforces Round #394 (Div. 2) C. Dasha and Password 暴力
C. Dasha and Password 题目连接: http://codeforces.com/contest/761/problem/C Description After overcoming ...
- Codeforces Round #258 (Div. 2) A. Game With Sticks 水题
A. Game With Sticks 题目连接: http://codeforces.com/contest/451/problem/A Description After winning gold ...
- Western Subregional of NEERC, Minsk, Wednesday, November 4, 2015 Problem I. Alien Rectangles 数学
Problem I. Alien Rectangles 题目连接: http://opentrains.snarknews.info/~ejudge/team.cgi?SID=c75360ed7f2c ...
- MikroTik RouterOS电子克隆盘原理收集
终于搞定RouteROS8位电子盘克隆,发个讯息出来分享一下. 不需要付费的免费分享,也没要刻意挡人财路:只是让信息流通一下. 也请看到的人不要用这个方式去赚钱,不然MikroTik还是会再反制的. ...
- 使用CefSharp在.Net程序中嵌入Chrome浏览器(七)——右键菜单
一个常用的功能就是禁止浏览器本身的右键菜单,靠在WPF中拦截鼠标事件是不行的,可以通过设置MenuHandler来实现. 首先实现一个IContextMenuHandler. public class ...
- 使用jqprint插件完成页面打印
使用jqprint插件完成页面打印 jqprint是一个基于jQuery编写的页面打印的一个小插件,但是不得不承认这个插件确实很厉害,最近的项目中帮了我的大忙,在Web打印的方面,前端的打印基本是靠w ...
- Spark RDD的fold和aggregate为什么是两个API?为什么不是一个foldLeft?
欢迎关注我的新博客地址:http://cuipengfei.me/blog/2014/10/31/spark-fold-aggregate-why-not-foldleft/ 大家都知道Scala标准 ...
