trie 树（字典树）

目录

• 简述
• trie 实现
  • 前言
  • 初始化
  • 插入
  • 检索
  • 代码实现
  • 例题 · 前缀统计
• 异或对
  • 前言
  • 贪心证明
  • 代码实现
  • 例题 · 最长异或值路径
• 可持久化 trie 树
  • 简介
  • 原理
  • 代码实现
  • 例题
• 总结

简述

trie 树（字典树）的名字告诉了我们一切，就是一颗像字典一样的树。

先不管怎么实现，先让我们了解它有什么用。

1. 实现字符串快速检索（“检”即看一个字符串有没有出现过，“索”即查看字符串相关信息）
2. 实现最大异或对相关问题（基于贪心思想，之后会讲）

当然，具体用处要看具体问题与具体情况，这里仅仅给出常用的两种方式。

接下来我们将一起探索 trie 树的实现。

trie 实现

前言

trie 树的本质是一颗多叉树，它的基础操作包括：初始化、插入与检索。

插入与检索的时间复杂度都为 \(O(c)\) （ \(c\) 为该字符串的长度），但是空间复杂度高达 \(O(nc)\) （\(n\) 为节点的个数）。

可见 trie 树对空间要求较高，这就要求同学们对于空间大小有准确的判断。

初始化

其实没什么好说的，没有特殊的初始化（都为 0 就可以了）。

唯一需要注意的是 \(tot=1\) ，\(tot\) 是什么之后再说，记住就可以了。

插入

当要插入一个字符串 \(S\) 是，令一个指针 \(P=1\) （即指向根节点），然后依次扫描 \(S\) 中的每一个字符 \(c\)：

1. 若 \(P\) 的 \(c\) 字符指针指向一个已经存在的节点 \(Q\) ，则令 \(P=Q\)。
2. 若 \(P\) 的 \(c\) 字符指针指向空，则新建一个节点 \(Q\) ，令 \(P\) 的 \(c\) 字符指针指向 \(Q\) ，然后 \(P=Q\)。

当 \(S\) 的字符扫描完毕时，在当前节点 \(P\) 上标记它是一个字符串的末尾。

注意： 在《算法竞赛进阶指南》中，用 \(end[]\) 数组标记字符串末尾，但 \(end\) 是 \(c++11\)的关键字，所以容易发生编译错误（可能本地编译没有问题，但提交就是不是到哪里错了），所以应换成其他名字。

代码如下：（这里没有改动 \(end []\) 数组，但考试时一定要改动）

void insert(string s){
	int len=s.length(),p=1;
	for(int i=0;i<len;i++){
		int ch=s[i]-'a';
		if(!trie[p][ch]) trie[p][ch]=++tot;
		p=trie[p][ch];
	}
	end[p]=true;//注意：end 数组并不可取，这里仅为了便于读者理解
	return;
}

这里出现了先前提到的 \(tot\) ，它指的是节点的编号总数，这里将根节点定义为 \(1\) ，所以之后的点从 \(2\) 开始。

（如果从 \(0\) 开始会有问题，原因留给读者思考）

检索

当需要检索一个字符串 \(S\) 是否存在时，令一个指针 \(P=1\) （即指向根节点），然后依次扫描 \(S\) 中的每一个字符 \(c\)：

1. 若 \(P\) 的 \(c\) 字符指针指向空，则说明 \(S\) 没有被插入过，结束检索。
2. 若 \(P\) 的 \(c\) 字符指针指向一个已经存在的节点 \(Q\) ，则令 \(P=Q\)。

当 \(S\) 的字符扫描完毕时，若当前节点 \(P\) 被标记为是一个字符串的末尾，return true，否则 return false。

代码如下：

bool search(string s){
	int len=s.length(),p=1;
	for(int i=0;i<len;i++){
		p=trie[p][s[i]-'a'];
		if(!p) return false;
	}
	return end[p];//同上
}

代码实现

完整代码如下：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<cstring>
#include<string>
#define N 100010
using namespace std;

int n,m,trie[N][30],tot=0;
bool end[N];
string a;

void insert(string s){
	int len=s.length(),p=1;
	for(int i=0;i<len;i++){
		int ch=s[i]-'a';
		if(!trie[p][ch]) trie[p][ch]=++tot;
		p=trie[p][ch];
	}
	end[p]=true;
	return;
}

bool search(string s){
	int len=s.length(),p=1;
	for(int i=0;i<len;i++){
		p=trie[p][s[i]-'a'];
		if(!p) return false;
	}
	return end[p];
}

int main(){
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++){
		cin>>a;
		insert(a);
	}
	for(int i=1;i<=m;i++){
		cin>>a;
		if(search(a)) printf("YES\n");
		else printf("NO\n");
	}
	return 0;
}

例题 · 前缀统计

前缀统计

trie 的简单运用仅仅有了一点点改变。

同样的把这 \(N\) 个字符串插入到 \(trie\) 中，在每个节点中记录一个 \(cnt\) 表示该节点是多少个字符串的末尾节点。

代码如下：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<iostream>
#define N 1000010
using namespace std;

int n,m,cnt[N],trie[N][30],tot=1;
char a[N];

void insert(char* a){
	int p=1,len=strlen(a);
	for(int i=0;i<len;i++){
		int ch=a[i]-'a';
		if(!trie[p][ch]) trie[p][ch]=++tot;
		p=trie[p][ch];
	}
	cnt[p]++;//唯一改变
	return;
}

int search(char* a){
	int p=1,len=strlen(a),ans=0;
	for(int i=0;i<len;i++){
		int ch=a[i]-'a';
		p=trie[p][ch];
		if(!p) return ans;
		ans+=cnt[p];
	}
	return ans;
}

int main(){
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%s",a);
		insert(a);
	}
	for(int i=1;i<=m;i++){
		scanf("%s",a);
		printf("%d\n",search(a));
	}
	return 0;
}

异或对

前言

如果这不提起，相信读者很难把 \(xor\) 与 \(trie\) 联系在一起。

简单说就是维护一个深度为 \(32\) 的多叉树，将每个数化为二进制数（\(int\) 的最大位数为 \(2^{32}-1\)，所以是 \(32\) 位）

接着枚举每一个数，与在 \(trie\) 中检索相类似的取查找，每次尽量找 \(xor A[i]\) 的一位就好（贪心）

贪心证明

这个贪心的正确性是很容易证明的，举个栗子：

1. \(A=“00000000”\)
2. \(B=“10000000”\)，\(AxorB=“10000000”\)
3. \(C=“01111111”\)，\(AxorC=“01111111”\)

那么按照贪心策略，\(A\) 的最大异或对为 \(AxorB\) （即使 \(B\) 只有第一位与 \(A\) 不同，\(AxorB\) 还是优于 \(AxorC\)）

代码实现

其实很好实现的，就只要按照上面说的做就好了：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<iostream>
#define N 100010
using namespace std;

int n,a[N],trie[N*32][5],tot=1;//注意trie[]大小的定义

void insert(int x){
	int p=1;
	for(int i=31;i>=0;i--){
		int ch=(x>>i)&1;//这里要求读者有一定位运算知识
		if(!trie[p][ch]) trie[p][ch]=++tot;
		p=trie[p][ch];
	}
	return;
}

int search(int x){
	int p=1,ans=0;
	for(int i=31;i>=0;i--){
		int ch=(x>>i)&1;//这里要求读者有一定位运算知识
		if(trie[p][ch^1]){
			ans|=(1<<i);//这里要求读者有一定位运算知识
			p=trie[p][ch^1];
		}
		else p=trie[p][ch];
	}
	return ans;
}

int main(){
	scanf("%d",&n);
	int sum=0;
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		insert(a[i]);
		sum=max(sum,search(a[i]));
	}
	printf("%d\n",sum);
	return 0;
}

例题 · 最长异或值路径

设 \(D[x]\) 表示根节点到 \(x\) 的路径上的所有边权的 \(xor\) 值，显然有：

\(D[x]=D[father(x)]\) \(xor\) \(weight(x,father(x))\)。

根据上式，我们可以先一遍 \(dfs\) 预处理出所有 \(D[x]\)。

不难很难发现，两个节点 \(x\) 与 \(y\) 之间的异或值等于 \(D[x]xorD[y]\) （原因是a xor a=0，所以两者之间的重合路径刚好抵消）

所以问题就变成了:

在 \(D[1]\) ~ \(D[N]\) 中选出两个数，使两者的 \(xor\) 结果最大（即上面的原题）

简单转化后，就可以发现问题与已学过问题的相似性（这是 \(OIer\) 所必备的能力，读者也要培养这种能力）

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#define N 100010
using namespace std;

int n,trie[N*32][2],tot=1,dis[N];
int head[N],cnt=0;
struct node{
	int next,to,val;
}edge[2*N];

void addedge(int x,int y,int z){
	cnt++;
	edge[cnt].next=head[x];
	edge[cnt].to=y;
	edge[cnt].val=z;
	head[x]=cnt;
	return;
}

void dfs(int x,int fa){

	for(int i=head[x];i;i=edge[i].next){
		int y=edge[i].to;
		if(y==fa) continue;
		int z=edge[i].val;
		dis[y]=dis[x]^z;
		dfs(y,x);
	}
	return;
}

void insert(int x){
	int p=1;
	for(int i=31;i>=0;i--){
		int ch=(x>>i)&1;
		if(!trie[p][ch]) trie[p][ch]=++tot;
		p=trie[p][ch];
	}
	return;
}

int search(int x){
	int p=1,ans=0;
	for(int i=31;i>=0;i--){
		int ch=(x>>i)&1;
		if(trie[p][ch^1]){
			ans|=(1<<i);
			p=trie[p][ch^1];
		}
		else p=trie[p][ch];
	}
	return ans;
}

int main(){
	scanf("%d",&n);
	int u,v,w;
	for(int i=1;i<n;i++){
		scanf("%d %d %d",&u,&v,&w);
		addedge(u+1,v+1,w);
		addedge(v+1,u+1,w);
	}
	dis[1]=0;
	dfs(1,0);
	int ans=0;
	for(int i=1;i<=n;i++){
		insert(dis[i]);
		ans=max(ans,search(dis[i]));
	}
	printf("%d\n",ans);
	return 0;
}

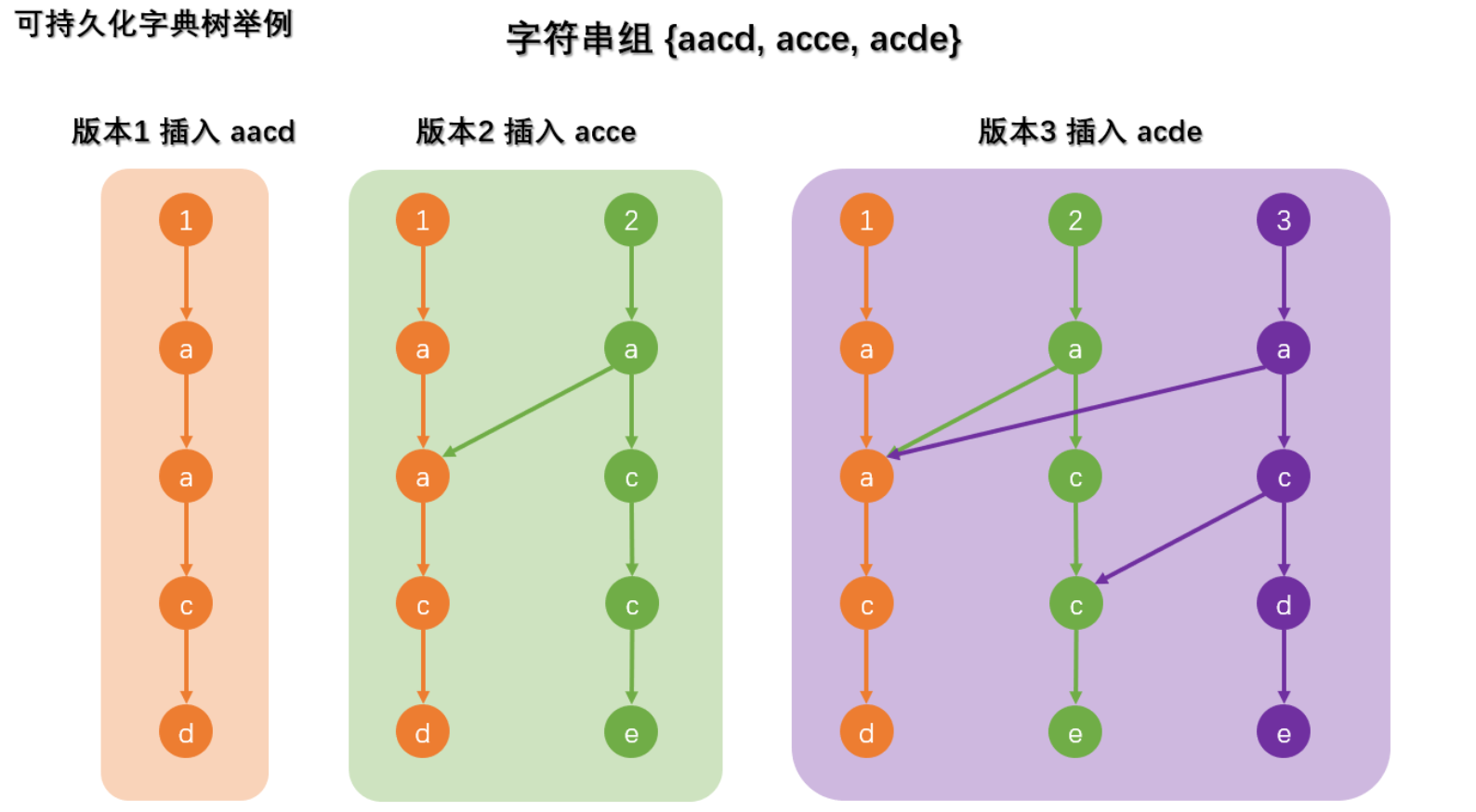
可持久化 trie 树

简介

\(Update\ on\ 2020.4.1\)

愚人节快乐...（话说你谷的愚人节比赛可真是 \(orz\)）

首先我们知道 \(trie\) 是一个灵活的数据结构，但是如果我要求求出在第 \(i\) 步插入之前单词 \(s[]\) 是否存在，怎么办呢？

我们发现之前的 \(trie\) 都是保存着当前最新状态，并没有保留历史状态，所以显然无法胜任这项工作。

这时，最简单的想法就是...开一个 \(history[]\) 存储每一棵历史上的 \(trie\)。

当然在大多数情况下等待着你的是 \(MLE\)...。所以就需要这种 高级 数据结构：可持久化 trie。

原理

易得我们现在的主要目标是减少空间开销，所以我们可以尝试仅仅存储与之前不同的（产生变化的）部分。

这样时间复杂度不变，空间复杂度仅仅随时间增长，高效的实现了保留历史记录的功能。

（网源图片，侵权请删）

就是酱紫...

代码实现

代码过于简单，不做过多介绍...（好吧是我太懒了），还是说两句吧。

可持久化 \(trie\) 的本质是一张 有向图，插入的过程分为以下几步。

1. 设当前的节点为 \(root\)，令 \(p=root,k=0\)。（\(k\) 表示遍历到当前字符串的哪一个字符）
2. 建立一个新节点 \(q\)，令 \(root'=q\)。（即 \(q=++tot\)）
3. 若 \(p\neq 0\)，对于每中字符 \(c\)，\(if(c\neq s[k])\ trie[q][c]=trie[p][c]\)。（就是将 \(trie[p][]\) 复制一遍）
4. 为当前字符建立一个新节点，令 \(trie[q][s[k]]=++tot\)。
5. 令 \(p=trie[p][s[k]],q=trie[q][s[k]],k++\)。
6. 重复上述步骤 \(3\)~\(5\)，直到 \(i=strlen[s]\)。

如此简单，代码就不贴了。

例题

一道相当经典的用可持久化 \(trie\) 解决的题目。

最大异或和

已知 \(trie\) 与 \(xor\) 有不解之缘，同样的，可持久化也可以用于解决 \(xor\) 问题。

因为 \(xor\) 满足区间可减性，即：

\[a_k\bigoplus a_{k+1}\bigoplus ...\bigoplus a_n=a_{k-1}\bigoplus \bigoplus^{n}_{i=1} a_i
\]

所以：\(a[p] \bigoplus a[p+1] \bigoplus ... \bigoplus a[n] \bigoplus x=s[p−1] \bigoplus s[n] \bigoplus x\)。（其中 \(s[i]=\bigoplus_{i=1}^n a_i\)）

此时查询转变为：已知 \(val=\mathrm{s[n]\ xor\ x}\)，求一个 \(p\in[l-1,r-1]\)，使得 \(\mathrm{s[p]\ xor\ val}\)最大。

可以构建一颗可持久化 \(\mathrm{Trie}\)，第 \(i\) 个版本为插入了 \(s[i]\) 后的 \(\mathrm{Trie}\) 树。

每次查询，从根节点开始，贪心地选与这一位相反的值。（贪心证明参见上文）

此外，还有一个 \(l-1\leq p\leq r-1\) 的限制。

先考虑 \(p\leq r-1\)，查询第 \(r-1\) 个版本的 \(\mathrm{Trie}\) 即可，因为此时不可能访问到 \(r-1\) 之后的 \(s[]\)。

再考虑 \(l-1\leq p\)，对每个节点维护一个 \(latest[]\)值，表示子树中所有 \(s\) 值的下标的最大值。

这样，在查询时只访问 \(latest\geq l-1\) 的节点就行了。

上代码：

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<iostream>
#define N 600010
using namespace std;

int n,m,s[N],root[N],tot=0;
int trie[N*24][2],latest[N*24];

int read(){
	int x=0,f=1;char c=getchar();
	while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
	while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
	return x*f;
}

void insert(int i,int k,int p,int q){
	if(k<0){
		latest[q]=i;
		return;
	}
	int c=s[i]>>k & 1;
	if(p) trie[q][c^1]=trie[p][c^1];
	trie[q][c]=++tot;
	insert(i,k-1,trie[p][c],trie[q][c]);
	latest[q]=max(latest[trie[q][0]],latest[trie[q][1]]);
	return;
}

int ask(int p,int val,int k,int limit){
	if(k<0) return s[latest[p]]^val;
	int c=val>>k & 1;
	if(latest[trie[p][c^1]]>=limit)
		return ask(trie[p][c^1],val,k-1,limit);
	else
		return ask(trie[p][c],val,k-1,limit);
}

int main(){
	n=read();m=read();
	int l,r,x;
	root[0]=++tot;
	latest[0]=-1;
	insert(0,23,0,root[0]);
	for(int i=1;i<=n;i++){
		x=read();
		s[i]=s[i-1]^x;
		root[i]=++tot;
		insert(i,23,root[i-1],root[i]);
	}
	char str[2];
	for(int i=1;i<=m;i++){
		scanf("%s",str);
		if(str[0]=='A'){
			x=read();
			root[++n]=++tot;
			s[n]=s[n-1]^x;
			insert(n,23,root[n-1],root[n]);
		}
		else{
			l=read();r=read();x=read();
			printf("%d\n",ask(root[r-1],x^s[n],23,l-1));
		}
	}
	return 0;
}

总结

在解决字符串相关问题以及异或对相关问题是可以往 trie 树一方面想一想。

当然只有这么多的做题量是远远不够的，请读者务必自己寻找更多相关习题。

注：

1. 全篇大多思想均来自：《算法竞赛进阶指南》。
2. 可持久化 \(trie\) 例题部分 部分讲解来自 这篇博客

完结撒花。