Representation Data in OpenCascade BRep

eryar@163.com

摘要Abstract：现在的显示器大多数是光栅显示器，即可以看做一个像素的矩阵。在光栅显示器上显示的任何图形，实际上都是一些具有一种或多种颜色的集合。数学上精确表示的图形在显示器中只能用逼近的方式显示出来。本文主要对OpenCascade的BRep文件中用来显示曲线和曲面的离散数据结构进行说明。

关键字：OpenCascade, BRep, Polygon, Triangulation, Subdivision Curves,

一、引言 Introduction

光栅图形显示器可以看做一个像素矩阵。在光栅显示器上显示的任何一种图形，实际上都是一些具有一种或多种颜色的像素的集合。在数学上，理想的曲线是没有宽度的，它是由无数个点构成的集合，而当要显示曲线时，就不能用无数个点在显示器中显示，必须对其进行离散化，即细分处理。考虑性能要求，需要用尽可能少的点来显示曲线。对于曲面也是一样，虽然已经有曲面的数学解析表示，但是需要在显示器中显示时，必须对其离散化，即三角剖分得到的逼近曲面的三角网格。

在OpenCascade中已经有曲线和曲面的精确的数学解析表达形式的类，如下图所示：

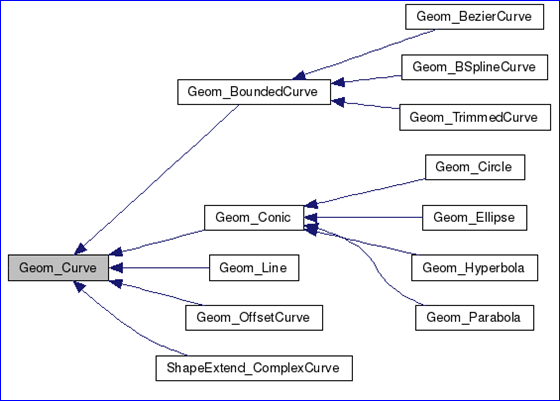
Figure 1.1 Parametric geometry curves

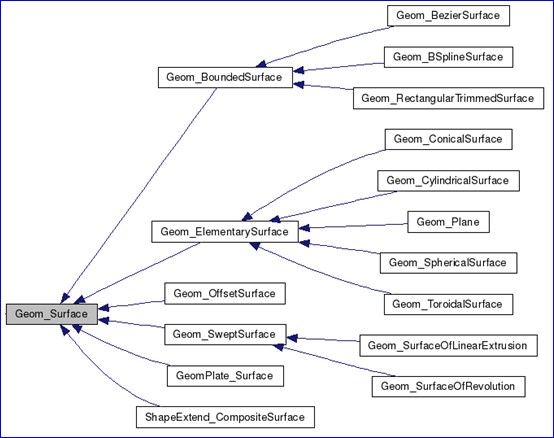
Figure 1.2 Parametric geometry surfaces

在OpenGL中显示这些曲线和曲面时，不能直接显示出由参数方程精确表示的曲线和曲面，必须对曲线和曲面进行细分，即离散化，得到OpenGL显示用的点和三角网格。

在OpenCascade中使用类Poly_Polygon3D/Poly_Polygon2D来保存多段线的数据，即可以用来保存逼近显示由参数方程精确表示的曲线的离散点数据。

在OpenCascade中使用类Poly_Triangulation来保存网格数据，即用三角网格来逼近表示的曲面，或更通用的一个形状。

形状的离散化由函数BRepMesh::Mesh()来统一处理，处理后就可以得到形状用来显示的多段线和三角网格数据。有了这些离散数据，不管是将形状交给显示模块进行显示，还是将形状在其他显示引擎中显示，就很方便了。

在OpenCascade的BRep中也保存了形状的用来显示用的离散数据，即多段线和三角网格。只有经过BRepMesh::Mesh()离散化之后，形状才具有这些数据。

二、细分曲线 Subdivision of Curves

在前面的一篇文章《在OpenSceneGraph中绘制OpenCascade的曲线》中对曲线的显示使用了统一细分处理（uniform subdivision），即将曲线在整个参数区域内均分后得到一些线段来显示。没有考虑这样的问题：在曲线很平的区域内，就会存在冗余的点；在曲线曲度很大的区域内，可能点的数量还不足以显示出光滑的曲线。自适应细分（Adaptive Subdivision）的方法就是将点放在最需要的地方，其主要目的是可视化曲线时更高效的渲染。通常这种方法主要用于游戏，因为其显示更高效，性能更好。

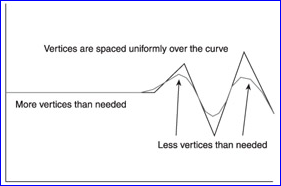
Figure 2.1 Uniform sampling on a curve

如上图所示，统一采样来绘制曲线时，通常会在直线段区域生成很多多余的点，而在曲线区域的点太少，不能表示出光滑的曲线。自适应细分曲线有很多种方法，每种方法都会考虑速度、效率和精度，即如何用最少的点精确地表示出曲线。当你理解这个基本概念后，也可以对其他方法进行研究。

在OpenCascade中对曲线的细分使用的类是GCPnts_TangentialDeflection，其算法描述如下，感兴趣的读者可以结合源程序对其算法实现进行研究：

其中各个点的横坐标对应的参数分别为：

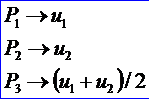
从上述公式结合向量的数量积公式可以看出，约束条件是两个向量夹角的余弦值分别小于角度偏差和曲率偏差。算法将产生满足约束条件的曲线上的最少数量的点。

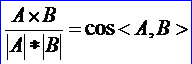
细分曲线后的点保存在类Poly_Polygon3D中。在BRep中也保存有多段线数据，如下所示：

示例：

BNF定义：

详细说明：

<3D polygon record>定义了空间多段线（3D polyline）L，用来逼近空间参数曲线C。多段线的数据包含节点数m>=2，参数显示标志位p，逼近偏差（deflection）d>=0，节点Ni（1=<i<=m），参数ui（1=<i<=m）。当参数显示标志位p＝1时，参数u才会显示。多段线L通过这些节点，多段线L逼近曲线C的逼近偏差定义如下所示：

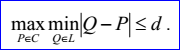
参数ui（1=<i<=m）是曲线C上通过节点Ni的参数值：

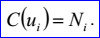
示例数据表示的多段线为：m＝2，参数显示标志位p＝1，逼近偏差d＝0.1，节点N1＝（1，0，0），N2＝（2，0，0），参数u1＝0，u2＝1。

三、细分曲面 Subdivision of surfaces

我们知道使用参数方程可以精确表示出三维曲线和曲面，但是参数方程表示的曲线曲面并不能直接交给OpenGL直接显示出来。为此，图形学中广泛使用三角网格来表达三维模型，即用三角形组成的面片列表来近似逼近表示三维模型。

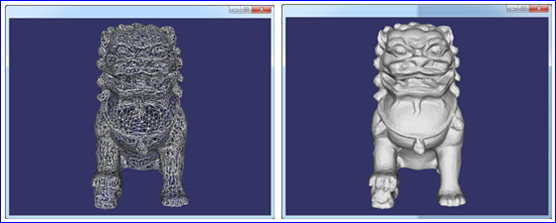
Figure 3.1 Triangulation of Chinese Dragon

用三角网格表示的曲面需要解决几个问题：三角网格的产生、描述、遍历、简化和压缩等。在OpenCascade中三角网格的产生使用算法Delaunay三角剖分算法生成网格数据，网格的描述使用类Poly_Triangulation。BRep文件中也保存三角网格的数据，如下所示：

示例：

BNF定义：

详细说明：

<triangulation record>定义了逼近曲面S的三角剖分T（triangulation）。三角剖分的数据包含节点数m>=3，三角形数k>=1，参数显示标志位p，逼近偏差d>=0，节点Ni（1<=i<=m），参数对ui,vi（1<=i<=m），三角形nj,1，nj,2，nj,3。参数只有当参数显示标志位p＝1时才显示。三角剖分逼近曲面的偏差d定义如下所示：

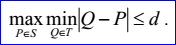
参数对ui，vi描述了曲面S上过节点Ni的参数：

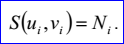
三角形nj,1， nj,2， nj,3用来取得三角形的三个顶点值Nnj,1，Nnj,2，Nnj,3，节点遍历的顺序就是Nnj,1，Nnj,2，Nnj,3。从三角剖分T的任意一侧遍历，所有三角形都有相同的方向：顺时针或逆时针。

三角剖分中的三角形数据：

表示的三角剖分为：m＝4个节点，k＝2个三角形，参数显示标志位p＝1，逼近偏差d＝0，节点N1（0，0，0），N2（0，0，3），N3（0，2，3），N4（0，2，0），参数值（u1,v1）＝（0，0），（u2,v2）＝（3，0），（u3,v3）＝（3，－2），（u4,v4）＝（0，－2）。从点（1，0，0）（（－1，0，0）），三角形是顺时针（逆时针）的。

四、程序示例 Code Example

通过创建多段线和三角网格数据并将其输出，可以理解BRep文件中用来显示的离散的数据结构。程序示例如下所示：

/*

*    Copyright (c) 2013 eryar All Rights Reserved.

*

*        File    : Main.cpp

*        Author  : eryar@163.com

*        Date    : 2013-12-12 21:46

*        Version : 1.0v

*

*    Description : There are two kind of data for shape representation

*                  of the BRep file of OpenCascade. One is Polyline to

*                  approximates a 3D curve; the other is triangulations

*                  to approximates a surface.

*

*       KeyWords : OpenCascade, BRep File, Polygon, Triangulation

*

*/

#define WNT

#include <TColStd_Array1OfReal.hxx>

#include <TColgp_Array1OfPnt.hxx>

#include <TColgp_Array1OfPnt2d.hxx>

#include <Poly.hxx>

#include <Poly_Polygon3D.hxx>

#include <Poly_Array1OfTriangle.hxx>

#include <Poly_Triangulation.hxx>

#pragma comment(lib, "TKernel.lib")

#pragma comment(lib, "TKMath.lib")

int main(void)

{

    // 3D Polygons:

    // Polygon3D 1

    // 2 1

    // 0.1

    // 1 0 0 2 0 0

    // 0 1

    TColStd_Array1OfReal parameters(, );

    TColgp_Array1OfPnt nodes(, );

    Handle_Poly_Polygon3D polyline;

    nodes.SetValue(, gp_Pnt(, , ));

    nodes.SetValue(, gp_Pnt(, , ));

    parameters.SetValue(, 0.0);

    parameters.SetValue(, 1.0);

    polyline = new Poly_Polygon3D(nodes, parameters);

    polyline->Deflection(0.1);

    Poly::Write(polyline, std::cout);

    Poly::Write(polyline, std::cout, false);

    // Triangulations.

    // 4 2 1 0

    // 0 0 0 0 0 3 0 2 3 0 2 0 0 0 3 0 3 -2 0 -2 2 4 3 2 1 4

    Standard_Integer nodeCount = ;

    Standard_Integer triangleCount = ;

    Standard_Real deflection = 0.0;

    Standard_Boolean hasUV = Standard_True;

    TColgp_Array1OfPnt triNodes(, nodeCount);

    TColgp_Array1OfPnt2d UVNodes(, nodeCount);

    Poly_Array1OfTriangle triangles(, triangleCount);

    Handle_Poly_Triangulation triangulation;

    triNodes().SetCoord(, , );

    triNodes().SetCoord(, , );

    triNodes().SetCoord(, , );

    triNodes().SetCoord(, , );

    UVNodes().SetCoord(0.0, 0.0);

    UVNodes().SetCoord(3.0, 0.0);

    UVNodes().SetCoord(3.0, -2.0);

    UVNodes().SetCoord(0.0, -2.0);

    triangles().Set(, , );

    triangles().Set(, , );

    triangulation = new Poly_Triangulation(triNodes, UVNodes, triangles);

    triangulation->Deflection(deflection);

    Poly::Write(triangulation, std::cout);

    Poly::Write(triangulation, std::cout, false);

    return ;

}

输出结果如下所示：

Poly_Polygon3D

0.1

Poly_Polygon3D

        Nodes

with parameters

Deflection : 0.1

Nodes :

          :

          :                                                   

Parameters :

Poly_Triangulation

 -

 -

Poly_Triangulation

        Nodes

        Triangles

with UV nodes

Deflection : 

3D Nodes :

          :

          :

          :

          :                                                   

UV Nodes :

          :

          :

          :                                 -

          :                                 -

Triangles :

          :

          :

Press any key to continue . . .

五、结论

通过对OpenCascade中BRep文件中的离散数据的学习，理解显示用数据结构及其实现。另外发现在类Poly和类BRepTools_ShapeSet中都有对多段线和三角网格进行读写的函数，有重复代码，可以合并简化。

PDF Version: Representation Data in OpenCascade BRep