题解 UVA12186 【工人的请愿书 Another Crisis】

俺太难了

记录一下我调了一个小时的错误

1. 多测不清空
2. 多测清空只清空了\(vector\)
3. 多测全清空了，但是忘了清空\(vector[0]\)
4. \(priority\)_ \(queue\)把\(greater\)打成了\(less\)

佛枯了

题解

这题都告了是树了

可以很容易的想到一个贪心策略：

某节点的儿子数是\(a[i]\)，则我们需要选\((a[i] * T - 1) / 100 + 1\)个子节点，那么现在这个节点的儿子数越少越好

另外，我们可以发现这题从根节点到子节点的时候不符合无后效性，举个栗子:

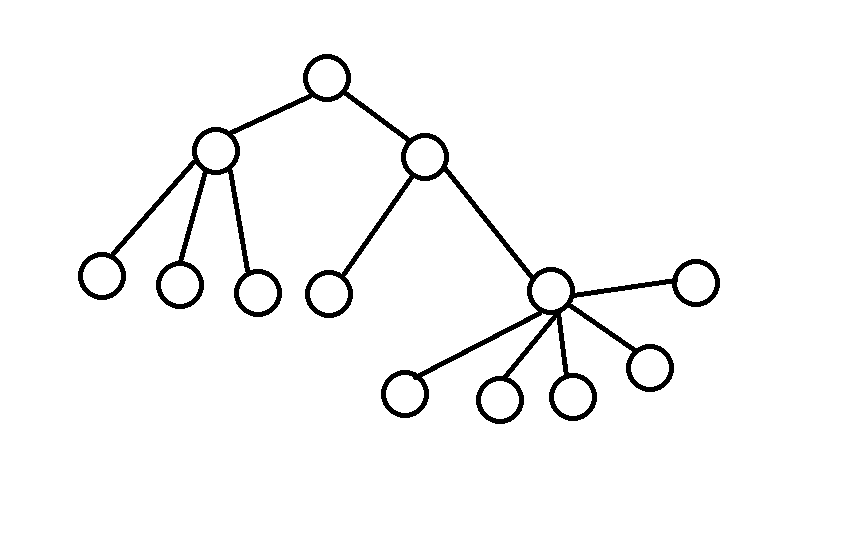
很显然选左边那棵子树是更优的，但是要是从上往下贪心的话我们就会选择右边的子树

所以我们只能从叶节点向根节点贪心

这个贪心我们用树上\(dp\)实现，用\(vector\)存图，用\(ans\)数组存选当前节点的话需要多少个叶节点

首先用\(vector\)存图，我们就能知道每个点的儿子的数量（不是子树大小)，接着从根向下\(dfs\)，顺手搞一个优先队列，回溯的时候顺带求出了\(ans\)数组，然后把\(ans\)数组放进优先队列，然后用前 \((a[i] * T - 1) / 100 + 1\) 小的子节点\(ans\)值更新当前点的\(ans\)值就可以了

代码如下

#include<bits/stdc++.h>
using namespace std;
#define rint register int
int n, T, ans[100010];
vector< int > a[100010];
inline int read( void ){
	int re = 0, f = 1;
	char ch = getchar();
	while( ch > '9' || ch < '0' ){
		if( ch == '-' ) f = -1;
		ch = getchar();
	}
	while( ch <= '9' && ch >= '0' ){
		re = re * 10 + ch - '0';
		ch = getchar();
	}
	return re * f;
}
inline void dfs( int now, int fa ){
	if( !a[now].size() ){
	ans[now] = 1; return ;
	}//边界条件
	priority_queue< int, vector< int >, greater< int > > que;
	for( rint i = 0; i < a[now].size(); i++ ){
		rint v = a[now][i];
		dfs( v, now );
		que.push( ans[v] );//入队
	}
	int tmp = ( a[now].size() * T - 1 ) / 100 + 1;//需要工人的个数
	for( rint i = 1; i <= tmp; i++ ){
		int v = que.top(); que.pop(); ans[now] += v;
	}
	return ;
}
int main( void ){
	while( 1 ){
		n = read(); T = read();
		for( rint i = 0; i <= n; i++ ) a[i].clear(); memset( ans, 0, sizeof( ans ) );
		if( n == 0 && T == 0 ) break ;
		for( rint i = 1; i <= n; i++ ){
			int temp; temp = read();
			a[temp].push_back( i );
		}
		dfs( 0, 0 );
		cout << ans[0] << endl;
	}
	return 0;
}