JavaScript数字精度丢失问题总结

本文分为三个部分

JS 数字精度丢失的一些典型问题
JS 数字精度丢失的原因
解决方案（一个对象+一个函数）

一、JS数字精度丢失的一些典型问题

1. 两个简单的浮点数相加

0.1 + 0.2 != 0.3 // true

Firebug

这真不是 Firebug 的问题，可以用alert试试（哈哈开玩笑）。

看看Java的运算结果

再看看Python

2. 大整数运算

9999999999999999 == 10000000000000001 // ？

Firebug

16位和17位数竟然相等，没天理啊。

又如

var x = 9007199254740992
x + 1 == x // ？

看结果

三观又被颠覆了。

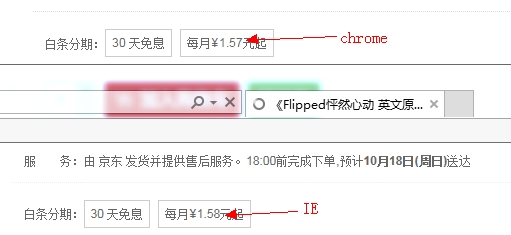
3. toFixed 不会四舍五入（Chrome）

1.335.toFixed(2) // 1.33

Firebug

线上曾经发生过 Chrome 中价格和其它浏览器不一致，正是因为 toFixed 兼容性问题导致

二、JS 数字丢失精度的原因

计算机的二进制实现和位数限制有些数无法有限表示。就像一些无理数不能有限表示，如圆周率 3.1415926...，1.3333... 等。JS 遵循 IEEE 754 规范，采用双精度存储（double precision），占用 64 bit。如图

意义

1位用来表示符号位
11位用来表示指数
52位表示尾数

浮点数，比如

0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
0.2 >> 0.0011 0011 0011 0011…（0011无限循环）

此时只能模仿十进制进行四舍五入了，但是二进制只有 0 和 1 两个，于是变为 0 舍 1 入。这即是计算机中部分浮点数运算时出现误差，丢失精度的根本原因。

大整数的精度丢失和浮点数本质上是一样的，尾数位最大是 52 位，因此 JS 中能精准表示的最大整数是 Math.pow(2, 53)，十进制即 9007199254740992。

大于 9007199254740992 的可能会丢失精度

9007199254740992     >> 10000000000000...000 // 共计 53 个 0
9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0
9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0

实际上

9007199254740992 + 1 // 丢失
9007199254740992 + 2 // 未丢失
9007199254740992 + 3 // 丢失
9007199254740992 + 4 // 未丢失

结果如图

以上，可以知道看似有穷的数字, 在计算机的二进制表示里却是无穷的，由于存储位数限制因此存在“舍去”，精度丢失就发生了。

想了解更深入的分析可以看这篇论文（又长又臭）：What Every Computer Scientist Should Know About Floating-Point Arithmetic

三、解决方案

对于整数，前端出现问题的几率可能比较低，毕竟很少有业务需要需要用到超大整数，只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。

对于小数，前端出现问题的几率还是很多的，尤其在一些电商网站涉及到金额等数据。解决方式：把小数放到位整数（乘倍数），再缩小回原来倍数（除倍数）

// 0.1 + 0.2
(0.1*10 + 0.2*10) / 10 == 0.3 // true

以下是我写了一个对象，对小数的加减乘除运算丢失精度做了屏蔽。当然转换后的整数依然不能超过 9007199254740992。

/**
 * floatObj 包含加减乘除四个方法，能确保浮点数运算不丢失精度
 *
 * 我们知道计算机编程语言里浮点数计算会存在精度丢失问题（或称舍入误差），其根本原因是二进制和实现位数限制有些数无法有限表示
 * 以下是十进制小数对应的二进制表示
 *      0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
 *      0.2 >> 0.0011 0011 0011 0011…（0011无限循环）
 * 计算机里每种数据类型的存储是一个有限宽度，比如 JavaScript 使用 64 位存储数字类型，因此超出的会舍去。舍去的部分就是精度丢失的部分。
 *
 * ** method **
 *  add / subtract / multiply /divide
 *
 * ** explame **
 *  0.1 + 0.2 == 0.30000000000000004 （多了 0.00000000000004）
 *  0.2 + 0.4 == 0.6000000000000001  （多了 0.0000000000001）
 *  19.9 * 100 == 1989.9999999999998 （少了 0.0000000000002）
 *
 * floatObj.add(0.1, 0.2) >> 0.3
 * floatObj.multiply(19.9, 100) >> 1990
 *
 */
var floatObj = function() {
 
    /*
     * 判断obj是否为一个整数
     */
    function isInteger(obj) {
        return Math.floor(obj) === obj
    }
 
    /*
     * 将一个浮点数转成整数，返回整数和倍数。如 3.14 >> 314，倍数是 100
     * @param floatNum {number} 小数
     * @return {object}
     *   {times:100, num: 314}
     */
    function toInteger(floatNum) {
        var ret = {times: 1, num: 0}
        var isNegative = floatNum < 0
        if (isInteger(floatNum)) {
            ret.num = floatNum
            return ret
        }
        var strfi  = floatNum + ''
        var dotPos = strfi.indexOf('.')
        var len    = strfi.substr(dotPos+1).length
        var times  = Math.pow(10, len)
        var intNum = parseInt(Math.abs(floatNum) * times + 0.5, 10)
        ret.times  = times
        if (isNegative) {
            intNum = -intNum
        }
        ret.num = intNum
        return ret
    }
 
    /*
     * 核心方法，实现加减乘除运算，确保不丢失精度
     * 思路：把小数放大为整数（乘），进行算术运算，再缩小为小数（除）
     *
     * @param a {number} 运算数1
     * @param b {number} 运算数2
     * @param digits {number} 精度，保留的小数点数，比如 2, 即保留为两位小数
     * @param op {string} 运算类型，有加减乘除（add/subtract/multiply/divide）
     *
     */
    function operation(a, b, digits, op) {
        var o1 = toInteger(a)
        var o2 = toInteger(b)
        var n1 = o1.num
        var n2 = o2.num
        var t1 = o1.times
        var t2 = o2.times
        var max = t1 > t2 ? t1 : t2
        var result = null
        switch (op) {
            case 'add':
                if (t1 === t2) { // 两个小数位数相同
                    result = n1 + n2
                } else if (t1 > t2) { // o1 小数位 大于 o2
                    result = n1 + n2 * (t1 / t2)
                } else { // o1 小数位 小于 o2
                    result = n1 * (t2 / t1) + n2
                }
                return result / max
            case 'subtract':
                if (t1 === t2) {
                    result = n1 - n2
                } else if (t1 > t2) {
                    result = n1 - n2 * (t1 / t2)
                } else {
                    result = n1 * (t2 / t1) - n2
                }
                return result / max
            case 'multiply':
            	result = (n1 * n2) / (t1 * t2)
                return result
            case 'divide':
            	result = (n1 / n2) * (t2 / t1)
                return result
        }
    }
 
    // 加减乘除的四个接口
    function add(a, b, digits) {
        return operation(a, b, digits, 'add')
    }
    function subtract(a, b, digits) {
        return operation(a, b, digits, 'subtract')
    }
    function multiply(a, b, digits) {
        return operation(a, b, digits, 'multiply')
    }
    function divide(a, b, digits) {
        return operation(a, b, digits, 'divide')
    }
 
    // exports
    return {
        add: add,
        subtract: subtract,
        multiply: multiply,
        divide: divide
    }
}();

toFixed的修复如下

// toFixed 修复
function toFixed(num, s) {
    var times = Math.pow(10, s)
    var des = num * times + 0.5
    des = parseInt(des, 10) / times
    return des + ''
}