图解汉诺塔问题（ Java 递归实现）

汉诺塔简介

最近在看数据结构和算法，遇到了一个非常有意思的问题——汉诺塔问题。

先看下百度百科是怎么定义汉诺塔的规则的：

汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

额，好吧，好像有点啰里啰嗦的。其实一句话就是，在三个柱子之间移动盘子，一次只能移动一个，并且要保证每一步上边的盘子都要比下边的盘子小，最终实现把所有的盘子都从最左边柱子移动到最右边的柱子上。

我找了一个小游戏，可以玩一下，体验一下这个过程。相信我，你玩不过第五关的！嘿嘿，玩不过再过来看一下，我是怎么给你做游戏攻略（作弊）的。

地址：http://www.4399.com/flash/109504_1.htm

我相信，有很多童鞋在学递归的时候，都会受到这个问题的困扰。别着急，你不是一个人，我第一次看到这个也是一脸懵逼，这什么鬼啊，这么复杂。下面我通过图解的方式，演示整个移动过程，帮助你理解用递归解决这个问题的思想。

汉诺塔图解

我们一步一步从简单到复杂。为了方便，我把三个柱子从左到右分别叫 A，B，C。盘子的数字从上到下依次增大。

一个盘子

只有一个盘子的时候，就比较简单了。如图，只需要一步，直接把第 1 个盘子从 A移动到 C就完成了。

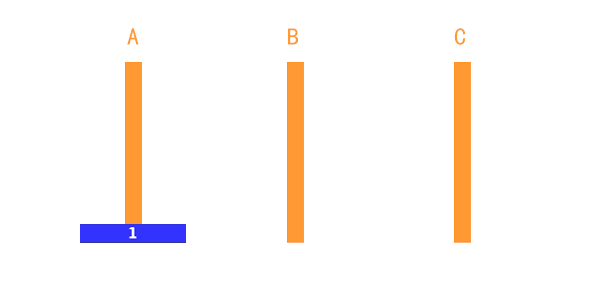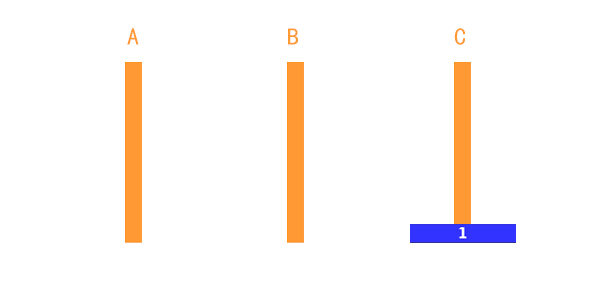
两个盘子

两个盘子的时候，也比较简单，如下图，只需要借助一下 B 柱子即可完成。

这个过程可以表述为：

把第1个盘子从A移到B
把第2个盘子从A移到C
把第1个盘子从B移到C

三个盘子

三个盘子的时候，稍微复杂一些，但是我们一般也是可以通过心算，把过程推演出来的。

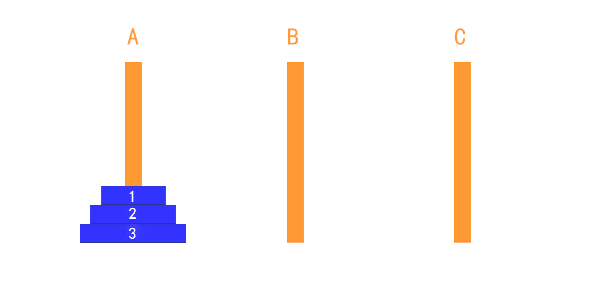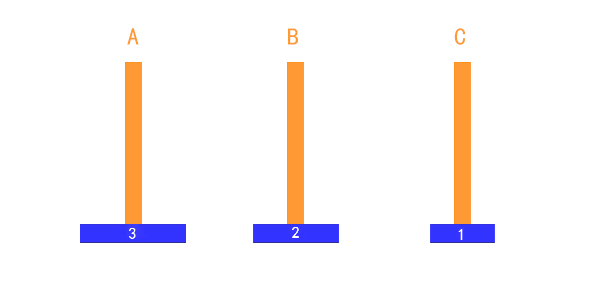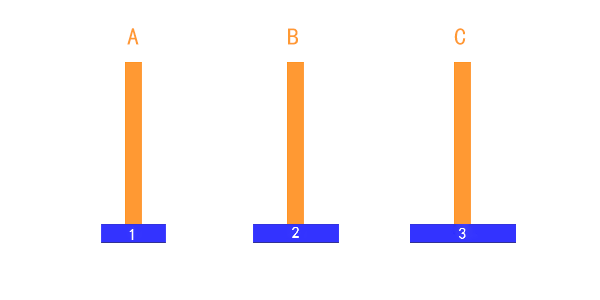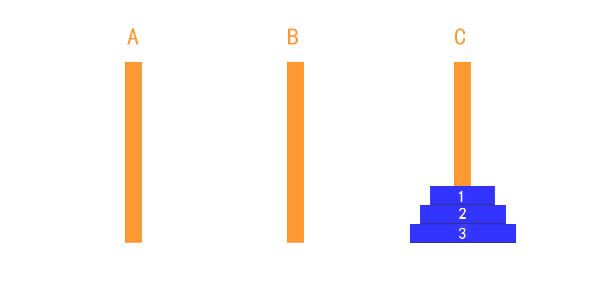
把第1个盘子从A移到C
把第2个盘子从A移到B
把第1个盘子从C移到B
把第3个盘子从A移到C
把第1个盘子从B移到A
把第2个盘子从B移到C
把第1个盘子从A移到C

n 个盘子

铛铛铛，现在到了第四关了，我相信已经有部分小伙伴感觉开始吃力了，通过演算就不好搞了。如果你搞不出来，我们就借助计算机来帮我们推算出来这个过程（哈哈，我是不是很机智）。

其实，通过前面的三个例子，我们可以发现，盘子的移动是有规律可循的。

细心的你有没有发现，在每一步盘子移动的过程中，总会有一步，是下边最大的盘子，从 A 移到 C 的。如，两个盘子，就是第 2 个盘子从 A移到 C，三个盘子，就是第 3 个盘子从 A 移到 C。

仔细观察，以三个盘子为例，把第 3 个盘子从 A 移动到 C 这一步，其实，第 1 个和第 2 个盘子是已经按顺序摆放好了的，即一起放在中间的 B 柱子。

因此，我们可以把这个动作抽象出来，把除了最下边的盘子之外的其他盘子看成一个整体。这样的话，整个流程，就和两个盘子的移动过程没什么两样了。总共就三步，我以四个盘子为例。看以下动画，

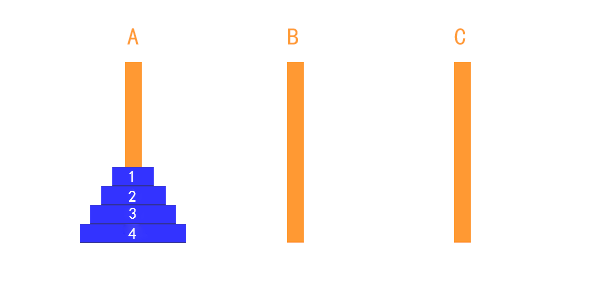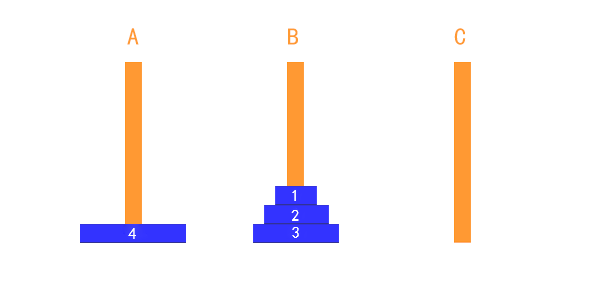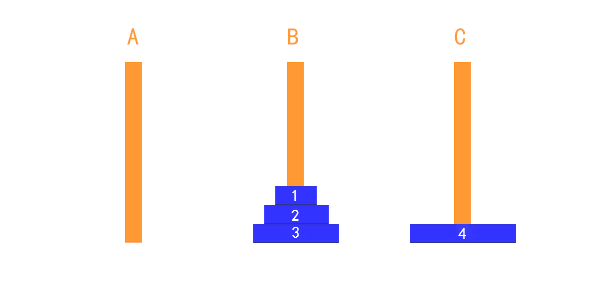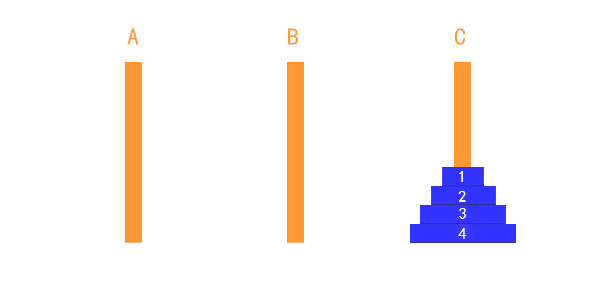
整个过程可以表述为：

把1,2,3盘子整体从 A 移到 B （可以认为是借助 C 柱子移动的），
把第 4 个盘子从 A 移到 C（不需要借助额外的柱子），
把1,2,3盘子整体从 B 移到 C（借助 A 柱子）

但是，这只是我们把它抽象出来的过程，游戏中不允许我们整体移动，怎么办呢。

好说，我把 1,2,3 这个整体再拆分，不就是三个盘子的移动过程嘛。完全可以把 1,2看成一个整体一起移动，3 单个移动，也是三步完成。然后再拆分，直到只有最后一个盘子的时候，就完成了整个过程。

所以，可以看到，这个拆分的过程，就是不断递归的过程。而每次递归时，都可以把第 1 个盘子到第 n-1 个盘子看成一个整体。每一次递归都是一个三步曲，借助另外一个柱子，从当前柱子移动到目标柱子。看代码，

public class HanioTest {
    public static void main(String[] args) {
        int n = 4;
        char a = 'A',b = 'B',c = 'C';
        hanio(n,a,b,c);
    }

    /**
     *
     * @param n  一共需要移动的盘子
     * @param a  盘子移动的起始柱子
     * @param b  借助的柱子
     * @param c  盘子需要移动到的目标柱子
     */
    public static void hanio(int n,char a, char b, char c){
        //只有一个盘子的时候，就直接从A移到C
        if(n == 1){
            move(n,a,c);
        }else{
            //三步曲，注意观察，a,b,c三个的位置变化
            //1.把 n-1 个盘子看成一个整体，借助 C 从 A 移动到 B
            hanio(n-1,a,c,b);
            //2.把第 n 个盘子从 A 移动到 C
            move(n,a,c);
            //3.再把 n-1 盘子整体，借助 A 从 B 移动到 C
            hanio(n-1,b,a,c);
        }
    }

    public static void move(int n , char a, char b){
        System.out.println("把第"+ n +"个盘子从"+ a +"移到"+ b);
    }
}

聪明的你，如果游戏第四关通关了，可以用来检查一下这个代码执行过程是否和你的移动过程一致。

第五关，如果你不借助程序，能心算出来，我只能说你太厉害了，I 服了 YOU，佩服佩服。

那么第六关，第七关呢。

结语

回到最开始，百度百科说要移动 64 片黄金圆盘，OMG 的，如果谁能手动计算出来，那才是真的大神（不过，话说，谁会这么无聊呢，哈哈）。

感兴趣的你也可以尝试用程序跑一遍 64 片是什么结果，我估计就算你机器性能很好，也得跑好长时间。。。

温馨提示：机器炸了不怪我哦 ~

如果本文对你有用，欢迎点赞，评论，转发。

学习是枯燥的，也是有趣的。我是「烟雨星空」，欢迎关注，可第一时间接收文章推送。