数学--数论--HDU 2802 F(N) 公式推导或矩阵快速幂

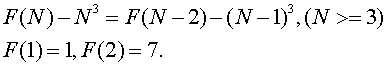
Giving the N, can you tell me the answer of F(N)?

Input

Each test case contains a single integer N(1<=N<=10^9). The input is terminated by a set starting with N = 0. This set should not be processed.

Output

For each test case, output on a line the value of the F(N)%2009.

Sample Input

1

2

3

0

Sample Output

1

7

20

打了个表 4018一循环

#include <bits/stdc++.h>
using namespace std;
int f[6000];
int main()
{
	f[1] = 1;
	f[2] = 7;
	for (int i = 3; i < 4020; i++)
	{
		f[i] = f[i - 2] + 3 * i * i - 3 * i + 1;
		f[i] %= 2009;
	}
	int n;
	while (scanf("%d", &n), n)
	{
		printf("%d\n", f[n % 4018]);
	}
}

或者矩阵快速幂分奇数偶数

#include "bits/stdc++.h"
using namespace std;
const int MOD = 2009;
const int MAT[][4] = {
    {1, 3, 3, 1},
    {0, 1, 4, 4},
    {0, 0, 1, 2},
    {0, 0, 0, 1}
};
const int TABLE1[] = {1, 4, 2, 1};
const int TABLE2[] = {7, 9, 3, 1};
struct Mat {
    int mat[4][4];
    Mat() {
        memset(mat, 0, sizeof(mat));
    }
    friend Mat operator * (Mat n, Mat m) {
        Mat res;
        for (int k = 0; k < 4; k++)
        for (int i = 0; i < 4; i++)
        for (int j = 0; j < 4; j++)
        res.mat[i][j] = (res.mat[i][j] + n.mat[i][k] * m.mat[k][j]) % MOD;
        return res;
    }
} m;
Mat mat_pow(Mat n, int k) {
    Mat res;
    for (int i = 0; i < 4; i++) {
        res.mat[i][i] = 1;
    }
    while (k) {
        if (k & 1) {
            res = res * n;
        }
        n = n * n;
        k >>= 1;
    }
    return res;
}
int main() {
    int n;
    while (scanf("%d", &n) && n) {
        if (n == 1) {
            puts("1");
            continue;
        }
        if (n == 2) {
            puts("7");
            continue;
        }
        memmove(m.mat, MAT, sizeof(m.mat));
        m = mat_pow(m, n - 1 >> 1);
        int res = 0;

        if (n & 1) {
            for (int i = 0; i < 4; i++) {
                res = (res + m.mat[0][i] * TABLE1[i]) % MOD;
            }
        } else {
            for (int i = 0; i < 4; i++) {
                res = (res + m.mat[0][i] * TABLE2[i]) % MOD;
            }
        }
        printf("%d\n", res);
    }
    return 0;
}