【BZOJ】2956：模积和

Time Limit: 10 Sec  Memory Limit: 128 MB

Description

求∑∑((n mod i)*(m mod j))其中1<=i<=n,1<=j<=m,i≠j。

Input

第一行两个数n,m。

Output

一个整数表示答案mod 19940417的值

Sample Input

3 4

Sample Output

1

样例说明
　　答案为(3 mod 1)*(4 mod 2)+(3 mod 1) * (4 mod 3)+(3 mod 1) * (4 mod 4) + (3 mod 2) * (4 mod 1) +

(3 mod 2) * (4 mod 3) + (3 mod 2) * (4 mod 4) + (3 mod 3) * (4 mod 1) + (3 mod 3) * (4 mod 2) +

(3 mod 3) * (4 mod 4) = 1

数据规模和约定
　　对于100%的数据n,m<=10^9。

这里是链接：【BZOJ】2956:模积和

这里是题解：

首先，暴力枚举将会很凄惨：O（nm）。早就 GG ( Time Limit Exceeded )了。

所以从公式入手：原公式是：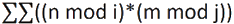

展开为：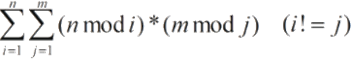

观察式子：[n mod i]（同理 m mod j）

根据mod的定义可以将上式写成这个样子：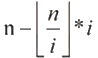

[n/i]向下取整，就是C++中的整型（n/i），然后再乘以 i 就相当于下图灰色区域，

再用n减掉就能得到mod后的值。【下图模拟mod的转化】

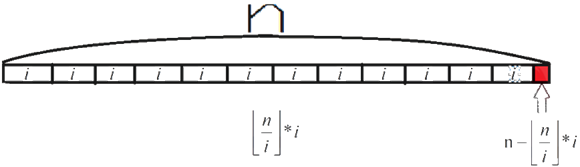
所以式子就可以简化为：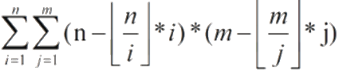

【注意：因为题目中i！=j，所以当i、j 相同就直接减掉】

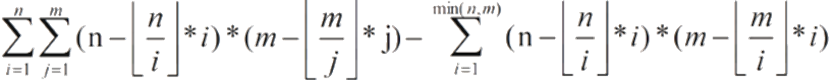
然而这样还是O(n^2)的复杂度。

所以继续化简：将第一个式子的Σ移动，使时间复杂度变为O(n)。

这里是最终式子：

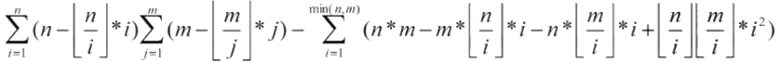
能够移动Σ的证明：设n-[n/i]*i为Xi,m-[m/j]*j为Yj。

（下图有点错误：n、m的值应该是不同的，但是n、m不同的证明也是这样的。）

这个是原式子展开的ans：

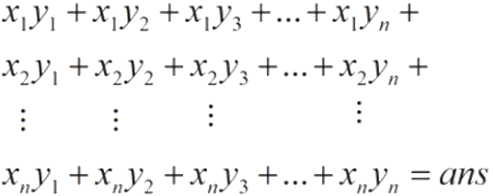
　　这个是化简后展开的ans：

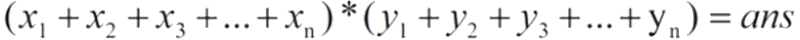
显然它们的ans值是相等的。那么，第一步化简式子已经完成了。

虽然移动Σ已经将复杂度降低到O（n），但很不幸的是依然过不了。

考虑如何优化：

低于O（n）的复杂度一般就三种：O（1）、O（logn）、O（√n）。

注意最终式子，都有一个式子like this：[n/i]（其中n为一个定值，i是从1到n的一个变量。）

但是这里有个很美妙的事情就是：

假如n==1000时，i在91~100之间，n/i的值都是为10的；

假如n==100000000时，i在9090910~10000000之间，n/i的值都是为10的。

这里因为在某一个区间中的值都是相等的。所以我们可以很愉快地利用分块的思想。

那么怎么算这个块的大小呢？

假设有一个块里面的[n/i]的值都是为k，那么其区间就是：[(n/(k+1))+1,n/k].

推导：因为[n/i]是向下取整的，所以k*i<=n，n/k为定值，所以i<=n/k，但i一定也有下界，所以i>n/(k+1)，

即i>=n/(k+1)+1.

注意：分块求值套用公式的时候需要除法，并不能先取模，然而不先取模会爆long long.

但好在除的数是固定的6，所以就直接在求平方和的时候，MOD开大6倍，最后再模回去就行了。

（其实反过来也就是网上普遍流传的3323403，是[mod/6]的值）

这里是代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define LL long long
#define mod 19940417
#define MOD 119642502
using namespace std;
LL n,m,tmp1,tmp2,ans,ine;

LL sum(LL x){
    return x*(x+)/%mod;
}

LL SUM(LL x){
    return x*(x+)%MOD*(*x+)%MOD/;
}

LL calc(LL x){
    LL ans=x*x%mod;
    for(LL i=;i<=x;i=tmp1+){
        tmp1=x/(x/i);//(x/i)求k的值，n/k为块的上界
         ans=(ans-(x/i)*(sum(tmp1)-sum(i-)+mod)%mod)%mod;
    }
    return ans%mod;
}

int main(){
    scanf("%lld %lld",&n,&m);
    if(n>m) swap(n,m);
    ans=calc(n)*calc(m)%mod;
    //处理i,j相同情况
    for(LL i=;i<=n;i=tmp2+){
        tmp2=min(n/(n/i),m/(m/i));
        ans=(ans-n*m%mod*(tmp2-i+)%mod
                +m*(n/i)%mod*(sum(tmp2)-sum(i-)+mod)%mod
                +n*(m/i)%mod*(sum(tmp2)-sum(i-)+mod)%mod
                -(n/i)*(m/i)%mod*(SUM(tmp2)-SUM(i-)+mod)%mod+*mod)%mod;
    }
    printf("%lld",ans%mod);
    return ;
}

【BZOJ】2956

梦想总是要有的，万一实现了呢？