洛谷 P1955 程序自动分析

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设x1,x2,x3...代表程序中出现的变量，给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：x1=x2,x2=x3,x3=x4,x4≠x1，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入输出格式

输入格式：

从文件prog.in中读入数据。

输入文件的第1行包含1个正整数t，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第1行包含1个正整数n，表示该问题中需要被满足的约束条件个数。接下来n行，每行包括3个整数i,j,e，描述1个相等/不等的约束条件，相邻整数之间用单个空格隔开。若e=1，则该约束条件为xi=xj；若�e=0，则该约束条件为xi≠xj；

输出格式：

输出到文件 prog.out 中。

输出文件包括t行。

输出文件的第 k行输出一个字符串“ YES” 或者“ NO”（不包含引号，字母全部大写），“ YES” 表示输入中的第k个问题判定为可以被满足，“ NO” 表示不可被满足。

输入输出样例

输入样例#1：

2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出样例#1：

NO
YES

说明

【样例解释1】

在第一个问题中，约束条件为：x1=x2,x1≠x2。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：x1=x2,x1=x2。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：x1=x2,x2=x3,x3=x1。只需赋值使得x1=x1=x1，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：x1=x2,x2=x3,x3=x4,x4≠x1。由前三个约束条件可以推出x1=x2=x3=x4，然而最后一个约束条件却要求x1≠x4，因此不可被满足。

【数据范围】

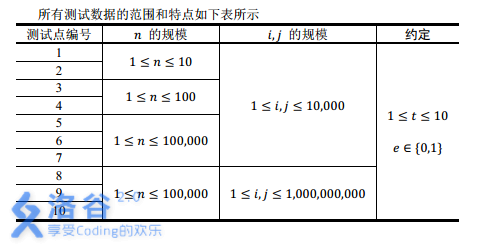
【时限2s，内存512M】

尽量不要用map map常数比较大

并查集+离散化

屠龙宝刀点击就送

#include <algorithm>
#include <cstring>
#include <cstdio>
#include <map>

using namespace std;
int num,T,cnt,fa[],c[];
struct node
{
    int a,b,c;
}e[];
bool flag=false;
int find_fa(int x){return x==fa[x]?x:fa[x]=find_fa(fa[x]);}
void qr(int &x)
{
    x=;bool f=;
    char ch=getchar();
    while(ch>''||ch<'')
    {
        if(ch=='-') f=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=x*+(int)ch-;
        ch=getchar();
    }
    x=f?(~x)+:x;
}
int main(int argc,char *argv[])
{
    qr(T);
    for(int n;T--;)
    {
        qr(n);
        cnt=;num=;flag=false;
        for(int i=;i<=n*;i++) fa[i]=i;
        for(int i=;i<=n;i++)
        {
            qr(e[i].a);qr(e[i].b);qr(e[i].c);
            c[++cnt]=e[i].a;
            c[++cnt]=e[i].b;
        }
        sort(c+,c++cnt);
        int size=unique(c+,c++cnt)-c-;
        for(int i=;i<=n;i++)
        {
            e[i].a=lower_bound(c+,c++size,e[i].a)-c;
            e[i].b=lower_bound(c+,c++size,e[i].b)-c;
        }
        for(int i=;i<=n;i++)
        {
            if(e[i].c==)
            {
                int fx=find_fa(e[i].a),fy=find_fa(e[i].b);
                if(fx!=fy) fa[fy]=fx;
            }
        }
        for(int i=;i<=n;i++)
        {
            if(!e[i].c)
            {
                int fx=find_fa(e[i].a),fy=find_fa(e[i].b);
                if(fx==fy)
                {
                    printf("NO\n");
                    flag=;
                    break;
                }
            }
        }
        if(!flag) printf("YES\n");
    }
    return ;
}