NOIP2013pj车站分级[拓扑排序]

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n 的 n 个火车站。每个火车站都有一个级

别，最低为 1 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车

次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。（注

意：起始站和终点站自然也算作事先已知需要停靠的站点）

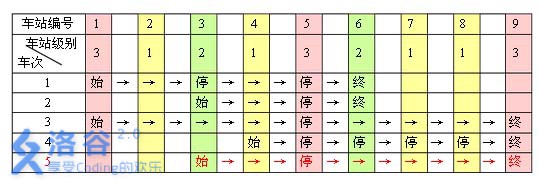
例如，下表是 5 趟车次的运行情况。其中，前 4 趟车次均满足要求，而第 5 趟车次由于

停靠了 3 号火车站（2 级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。

现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的

级别。

输入输出格式

输入格式：

输入文件为 level.in。

第一行包含 2 个正整数 n, m，用一个空格隔开。

第 i + 1 行（1 ≤ i ≤ m）中，首先是一个正整数 si（2 ≤ si

≤ n），表示第 i 趟车次有 si 个停

靠站；接下来有 si个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个

空格隔开。输入保证所有的车次都满足要求。

输出格式：

输出文件为 level.out。

输出只有一行，包含一个正整数，即 n 个火车站最少划分的级别数。

输入输出样例

输入样例#1：

Case 1:
9 2
4 1 3 5 6
3 3 5 6 

Case 2:
9 3
4 1 3 5 6
3 3 5 6
3 1 5 9

输出样例#1：

Case 1:
2

Case 2:
3

说明

对于 20%的数据，1 ≤ n, m ≤ 10；

对于 50%的数据，1 ≤ n, m ≤ 100；

对于 100%的数据，1 ≤ n, m ≤ 1000。

---

1.将所有入度读为零的点入栈。

2.将栈中所有点相连的边去掉，相连的点入度 --。

直到栈空，操作数为答案(相当于DAG最长环长度)

PS：起点终点不一定是1和n，太扯了

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=1e3+,INF=1e9+;
inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
int n,m,s,g[N][N],vis[N],lst[N],ind[N],ans=;
int st[N],top=,buf[N],top2=;
void toposort(){
    for(int i=;i<=n;i++) if(ind[i]==) st[++top]=i;
    while(top){
        ans++;//printf("hi %d %d\n",ans,del);
        while(top){
            int u=st[top--];  //printf("u %d\n",u);
            for(int v=;v<=n;v++) if(g[u][v]){
                ind[v]--;   //printf("v %d %d\n",v,ind[v]);
                if(ind[v]==) buf[++top2]=v;
            }
        }
        for(int i=;i<=top2;i++) st[i]=buf[i];
        top=top2;
        top2=;
    }
}
int main(){
    n=read();m=read();
    for(int i=;i<=m;i++){
        s=read();
        memset(vis,,sizeof(vis));
        for(int j=;j<=s;j++) lst[j]=read(),vis[lst[j]]=;
        for(int j=lst[];j<=lst[s];j++) if(!vis[j])
            for(int k=;k<=s;k++) if(!g[lst[k]][j]) g[lst[k]][j]=,ind[j]++;
    }
    toposort();
    printf("%d",ans);
}