[Elementary Mechanics Using Python-02]Feather in tornado

Problem

9.17 Feather in tornado.

In this project you will learn to use Newton’s laws and the force model for air resistance in a wind field to address the motion of a light object in strong winds. We start from a simple model without wind and gradually add complexity to the model, until we finally address the motion in a tornado. Motion without wind:

First, we address the motion of the feather without wind.

(a) Identify the forces acting on a feather while it is falling and draw a free-body diagram for the feather.

(b) Introduce quantitative force models for the forces, and find an expression for the acceleration of the feather. You may assume a quadratic law for air resistance.

(c) If you release the feather from rest, its velocity will tend asymptotically toward the terminal velocity, \(v_T\) . Show that the terminal velocity is \(v_T\) = \(−(mg/D)^{1/2}\), where D is the constant in the air resistance model.

(d) We release the feather from a distance h above the floor and measure the time t until the feather hits the floor. You may assume that the feather falls with a constant velocity equal to the terminal velocity. Show how you can determine D/mg by measuring the time t. Estimate D/mg when you release the feather from a height of 2.4 m above the floor and it takes 4.8 s until it hits the floor.

(e) We will now develop a more precise model where we do not assume that the velocity is constant. You release the feather from the height h at the time t = 0 s. Find the equation you have to solve to find the position of the feather as a function of time. What are the initial conditions?

(f) Write a program that solves this equation to find the velocity and position as a function of time t. Use the parameters you determined above, and test the program by ensuring that it produces the correct terminal velocity.

(g) Fig. 9.19 shows the position and velocity calculated with the program using the parameters found above. Was the approximation in part (d) reasonable? Explain your answer. Model with wind: We have now found a model that can be used to find the motion of the feather. We will now find the motion of the feather in three dimensions while it is blowing. The velocity of the wind varies in space, so that the wind velocity w is a function of the position r. We write this as w = w(r).

(h) Find an expression for the acceleration of the feather. The expression may include the wind velocity w(r). Let the z-axis correspond to the vertical direction.

(i) Assume that the feather is moving in an approximately horizontal plane—that is you may assume that the vertical acceleration is negligible. How does the wind have to blow in order for the feather to move in a circular orbit of radiusr0 with a constant speed v0?

Motion in a tornado: For a tornado with a center at the origin, the wind velocity is expected to be approximately given by the model:

\[\boldsymbol{w}(\boldsymbol{r}) = u_0\boldsymbol{r}e^{−r/R}\hat{u_θ} = u_0(-y, x,0)e^{−r/R}\hat{u_θ} , \space \space (9.79)
\]

where u0 is a characteristic velocity for the wind, R is the radius of the tornado, and uˆθ is a tangential unit vector in the horizontal plane (\(\hat{u_\theta}\) is normal to r). Here, r = (x, y,z), and r = |r|. The velocity field is illustrated in Fig. 9.20.

(j) Is is possible to choose an appropriate set of initial conditions so that the feather moves in a circular path in the tornado? Explain your answer.

(k) Rewrite your program to find the velocity and position of the feather as a function of time. For the tornado you may use the values u0 = 100 m/s and R = 20 m.

(l) Find the trajectory for the feather if it is released from rest from a height of 2.4m, and in a position corresponding to r = −R i + hk. (m) The trajectory of the feather is shown in Figs. 9.20 and 9.21. Compare the results with what happended when you dropped the feather without wind. Why does the feather now take longer to reach the ground?

Solution

\((a)\)

考虑无风情况，\(\boldsymbol{w} = \boldsymbol{0}\)，很容易画出受力分析图

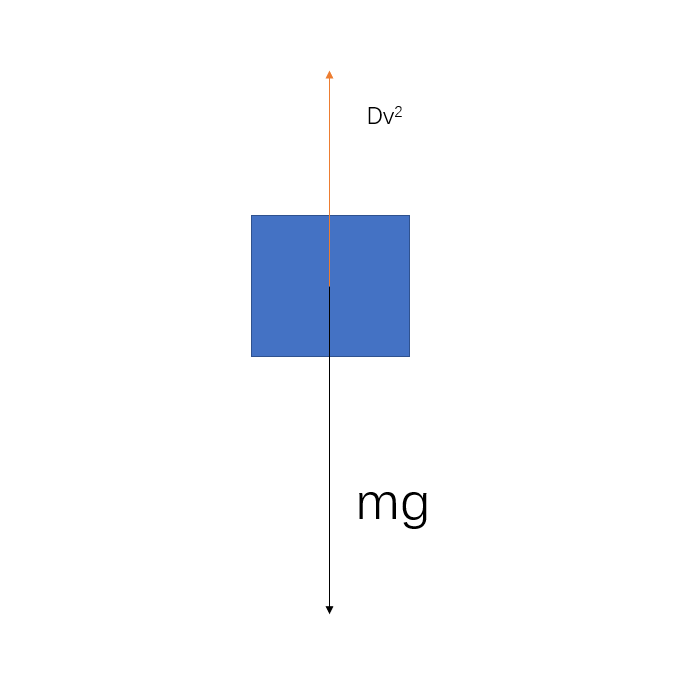
\((b)\)

由受力分析图可以简单的列出动力学方程

\[m\boldsymbol{a} = -mg\boldsymbol{k} - D|\boldsymbol{v}|\boldsymbol{v}
\]

\(\Rightarrow\)

\[\boldsymbol{a} = -(\boldsymbol{k} + \frac{D}{mg}|\boldsymbol{v}|\boldsymbol{v})g
\]

\((c)\)

我们令 \(\boldsymbol{a} = \boldsymbol{0}\), 得到方程

\[\boldsymbol{0} = -(\boldsymbol{k} + \frac{D}{mg}|\boldsymbol{v}|\boldsymbol{v})g
\]

\(\Rightarrow\)

\[\boldsymbol{v} = -\sqrt[]{\frac{mg}{D}}\boldsymbol{k} \\
\]

\((d)\)

由\((c)\)中公式，我们列出

\[v_T\times t = h
\]

将\(v_T = -\sqrt[]{\frac{mg}{D}}\)带入求解，得

\[\frac{D}{mg} = \frac{t^2}{h^2} = 4
\]

\((e)\)

此问方程就是\((b)\)中得到的方程

\[\boldsymbol{a} = -(\boldsymbol{k} + \frac{D}{mg}|\boldsymbol{v}|\boldsymbol{v})g
\]

\((f)\)

编程实现

import numpy as np
import matplotlib.pyplot as plt

G = 9.81
H = 2.4
dt = 0.001
C = 4               # D/mg

t = np.arange(0, 5, 0.001)
a = np.zeros(5000, dtype=float)
v = np.zeros(5000, dtype=float)
x = np.zeros(5000, dtype=float)

a[0] = -G
v[0] = 0
x[0] = H

for index in range(1, 5000):
    a[index] = (-1 + C*v[index-1]**2)*G
    v[index] = v[index-1] + a[index-1]*dt
    x[index] = x[index-1] + v[index-1]*dt

plt.subplot('211')
plt.title('$x(t)$')
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position(('data', 0))
plt.plot(t, x, label="$x(t)$")
plt.xlim([0, 5])
plt.ylim([0, 3])
plt.xlabel('$t[s]$')
plt.ylabel('$x[m]$')
plt.legend()

plt.subplot('313')
plt.title('$v(t)$')
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position(('data', 0))
plt.plot(t, v, label="$v(t)$")
plt.xlim([0, 5])
plt.ylim([-0.8, 0])
plt.xlabel('$t[s]$')
plt.ylabel('$v[m/s]$')
plt.legend()
plt.savefig('f.jpg', dpi=3000)

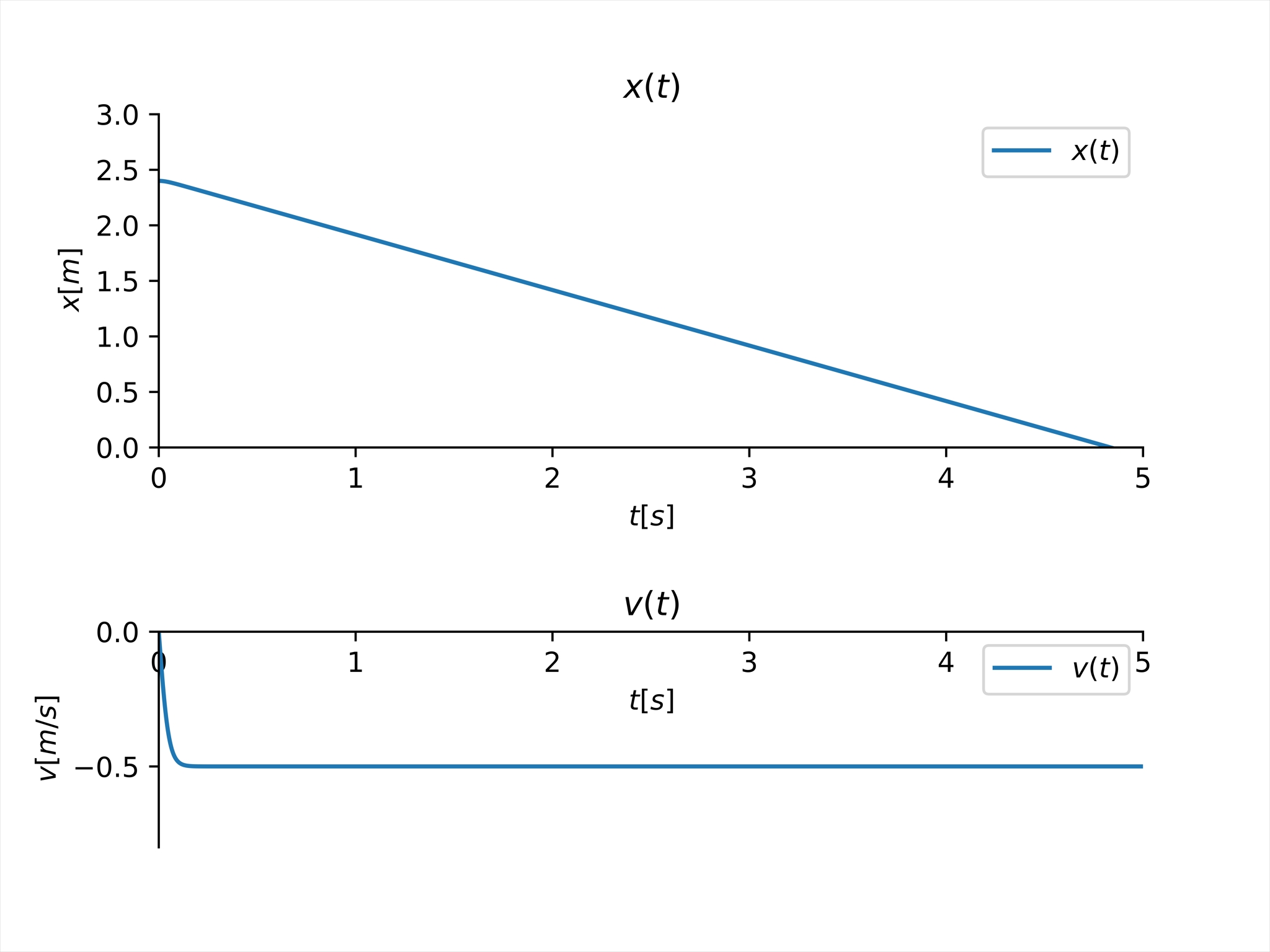
\((h)\)

考虑上风力，改为相对于风的速度

\[\frac{d\boldsymbol{v}}{dt} = -(\boldsymbol{k} + \frac{D}{mg}|\boldsymbol{v}-\boldsymbol{w}|(\boldsymbol{v}-\boldsymbol{w}))g\\
\]

\((i)\)

忽略铅锤方向加速度，\(让g \rightarrow 0, 且当\boldsymbol{a}=-\frac{v_0^2}{r_0}\hat{r}时：\\\)

\[-\frac{v_0^2}{r_0}\hat{r} = -\frac{D}{m}|\boldsymbol{v}-\boldsymbol{w}|(\boldsymbol{v}-\boldsymbol{w})\\
\]

解出\(\boldsymbol{w}\)

\[\boldsymbol{w}(r_0) = -\sqrt\frac{mv_0^2}{Dr_0} \hat{r}+v_0\hat{\theta} \\
\]

\((j)\)

首先列出羽毛的微分方程

\[\frac{d\boldsymbol{v}}{dt} = -(\boldsymbol{k} + \frac{D}{mg}|\boldsymbol{v}-\boldsymbol{w}|(\boldsymbol{v}-\boldsymbol{w}))g
\]

找到初值条件

\[\left\{\begin{matrix}\begin{align}
&\boldsymbol{x}(0) = [-20, 0, 2.4] \\
&\boldsymbol{v}(0) = [0, 0, 0] \\
&\boldsymbol{a}(0) = -(\boldsymbol{k} + \frac{D}{mg}|\boldsymbol{v}(0)-\boldsymbol{w}(\boldsymbol{x}(0))|(\boldsymbol{v}(0)-\boldsymbol{w}(\boldsymbol{x}(0))))g\\
\end{align}\end{matrix}\right.
\]

编程实现

import numpy as np
import matplotlib.pyplot as plt

// 定义常量
u0 = 100
R = 20
H = 2.4
G = 9.81
k = np.array([0, 0, 1])
C = 4 # D/mg

def Len(vector):
    return np.sqrt(vector[0]**2+vector[1]**2+vector[2]**2)
// 风场函数
def w(xVector, yVector, zVector=0):
    rLen = Len([xVector, yVector, zVector])
    return np.array([u0*np.exp(-rLen/R)*(-yVector), u0*np.exp(-rLen/R)*xVector, u0*np.exp(-rLen/R)*0])
// 加速度函数
def A(v, r):
    W = w(r[0], r[1], r[2])
    return -(k+C*(v - W)*Len((v - W)))*G
// 创建网格
xVector, yVector= np.meshgrid(
    np.linspace(-101, 101, 100),
    np.linspace(-101, 101, 100)
)
// 计算风场
uVector, vVector, wVector = w(xVector, yVector)
M = np.hypot(uVector,vVector)
// 绘制风场
plt.quiver(
    xVector, yVector,
    uVector, vVector,
    M, pivot='mid', width=0.001
)

dt = 0.00001
tMax = 30
t = np.arange(0, tMax, dt)
x = np.zeros((int(tMax/dt), 3))
v = np.zeros((int(tMax/dt), 3))
a = np.zeros((int(tMax/dt), 3))
// 初值条件
v[0,:] = np.array([0, 0, 0])
x[0,:] = np.array([-20, 0, H])
a[0,:] = A(v[0,:], x[0,:])
// 数值积分
i = 0
for index in range(1, 3000000):
    a[index,:] = A(v[index-1,:], x[index-1,:])
    v[index,:] = v[index-1,:] + a[index-1,:]*dt
    x[index,:] = x[index-1,:] + v[index-1,:]*dt
    if x[index,2] <= 0:
        i = index
        print("drop at {} s".format(i*dt))
        break
// 绘制羽毛轨迹
plt.plot(x[:i,0], x[:i,1], 'r', linewidth=0.5)
plt.scatter(x[:i:10000,0], x[:i:10000,1], s=0.6)
plt.xlim([-101, 101])
plt.ylim([-101, 101])
plt.axis('equal')
plt.savefig('1.jpg', dpi=3000)

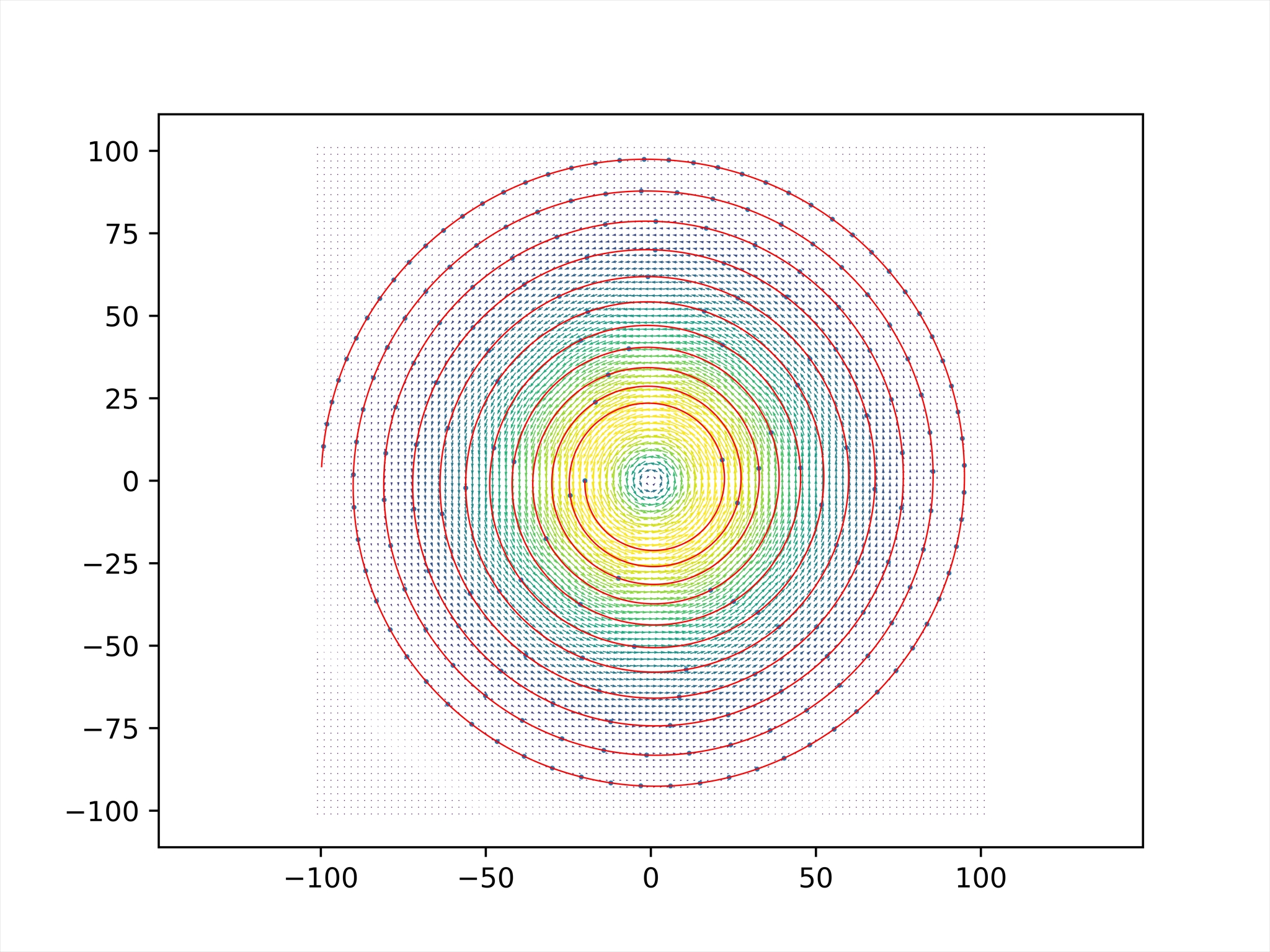
结论

在龙卷风影响下，计算出羽毛要经过 \(20.59065 s\) 落到地面，远大于无风情况下的情况，主要原因是采用了平方模型，使得空气阻力非线性。