hdu 6867 Tree 2020 Multi-University Training Contest 9 dfs+思维

题意：

给你一个由n个点，n-1条有向边构成的一颗树，1为根节点

下面会输入n-1个数，第i个数表示第i+1点的父节点。你可以去添加一条边（你添加的边也是有向边），然后找出来（x，y）这样的成对节点。问你最多能找出来多少对

其中x和y可以相等，且x点要可以到达y点

题解：

根据样例找一下就可以看出来让根节点1和深度最深那个点相连之后能找出来的（x，y）最多

但是又出现一个问题，如果那个最大深度的点不止一个，那么我们要选择那个。如下样例

6

1 1 2 2 3

化成图就是

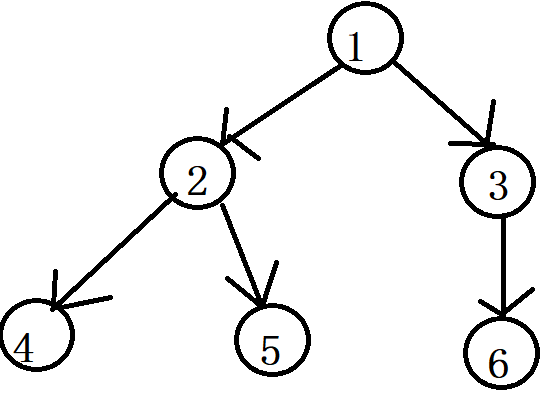
4、5、6号点都是最深深度的点，且如果你选择4或5和根节点1相连，那么（x，y）的数量是22，如果你选择6点和根节点1相连，那么（x，y）的数量是23

所以最深深度节点有多个我们还需要判断，于是我们先找到所有最深深度的点，然后对它们进行枚举

设最深深度为maxx，你会发现，答案的一部分是maxx*（n-1）+maxx

maxx*（n-1）：就是我们找到的那个最深深度那个点和根节点1构成的那个链，那个链上的所有点都可以到达其他顶点，所以就是这个答案

maxx：因为x和y可以相等，所以就加上这个链上的所有点

对于其他（x，y）我么可以这样找，我们还用上面的例子，我们找最长链为1，3，6

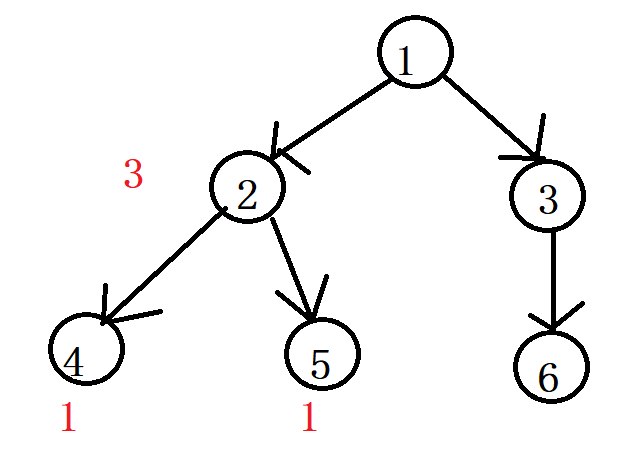
我们首先把1，3，6这条边标记，然后把没有标记链的红色权值加起来就行了，红色权值的构成就是每一个点最开始红色权值是1，然后子节点为父节点贡献它的权值，子节点向父节点贡献权值就相当于(2，4)和(2，5)。

它们本身最开始的权值1就相当于(4，4)，(5，5)，(2，2)

但是最后你会发现这样会TLE

TLE代码：

  1 #include<stack>
  2 #include<queue>
  3 #include<map>
  4 #include<cstdio>
  5 #include<cstring>
  6 #include<iostream>
  7 #include<algorithm>
  8 #include<vector>
  9 #define fi first
 10 #define se second
 11 #define pb push_back
 12 using namespace std;
 13 typedef long long ll;
 14 const int maxn=5e5+10;
 15 const int mod=1e9+7;
 16 const double eps=1e-8;
 17 ll vis[maxn],val[maxn],fa[maxn],test[maxn],head[maxn],summ[maxn];
 18 queue<ll>r;
 19 vector<ll>w[maxn];
 20 void add_edge(ll x,ll y)
 21 {
 22     w[x].push_back(y);
 23 }
 24 void dfs(ll x)
 25 {
 26     ll len=w[x].size();
 27     for(ll i=0;i<len;++i)
 28     {
 29         ll y=w[x][i];
 30         dfs(y);
 31         summ[x]+=summ[y];
 32     }
 33 }
 34 int main()
 35 {
 36     ll t;
 37     scanf("%lld",&t);
 38     while(t--)
 39     {
 40         while(!r.empty())
 41             r.pop();
 42         memset(vis,0,sizeof(vis));
 43         memset(test,0,sizeof(test));
 44         ll n,x,total,maxx=1,pos=1,index=1;
 45         scanf("%lld",&n);
 46         for(int i=1;i<=n;++i)
 47             w[i].clear();
 48         fa[1]=0;
 49         val[1]=1;
 50         summ[1]=1;
 51         for(ll i=2; i<=n; ++i)
 52         {
 53             summ[i]=1;
 54             scanf("%lld",&fa[i]);
 55             add_edge(fa[i],i);
 56             val[i]=val[fa[i]]+1;
 57             test[fa[i]]=i;
 58             if(maxx<val[i])
 59             {
 60                 maxx=val[i];
 61                 pos=i;
 62             }
 63         }
 64         dfs(1);
 65 //        for(ll i=2; i<=n; ++i)
 66 //        {
 67 //            if(test[i]==0)
 68 //            {
 69 //                head[index++]=i;
 70 //                ll temp=i;
 71 //                while(fa[temp])
 72 //                {
 73 //                    summ[fa[temp]]+=summ[temp];
 74 //                    temp=fa[temp];
 75 //                }
 76 //            }
 77 //        }
 78         for(ll i=2; i<=n; ++i)
 79         {
 80             if(val[i]==maxx)
 81             {
 82                 r.push(i);
 83             }
 84         }
 85         ll result=0;
 86         ll bloo=maxx*(n-1)+maxx;
 87         //printf("%d %lld\n",r.size(),maxx*(n-1)+n);
 88         while(!r.empty())
 89         {
 90             ll temp=r.front(),sum=bloo;
 91             while(temp)
 92             {
 93                 vis[temp]=1;
 94                 temp=fa[temp];
 95             }
 96             temp=r.front();
 97             for(ll i=2;i<=n;++i)
 98             {
 99                 if(vis[i]==0)
100                 {
101                     sum+=summ[i];
102 //                    if(temp==8)
103 //                    {
104 //                        printf("%lld %lld\n",i,summ[i]);
105 //                    }
106                 }
107
108             }
109             result=max(result,sum);
110             temp=r.front();
111             r.pop();
112             while(temp)
113             {
114                 vis[temp]=0;
115                 temp=fa[temp];
116             }
117         }
118         printf("%lld\n",result);
119     }
120     return 0;
121 }
122 /*
123
124 */

然后就想办法优化，你可以先把所有节点的红色权值都算出来，然后把这些值都加起来，使用变量k保存，然后我们用一个数组变量

sumi表示从根节点到i节点所有节点红色权值的和

对于我们枚举到的一个最深深度节点i，我们可以使用k-sum[i]来找出来排除最长链之外的其他点能找到的（x，y）

然后再加上之前的maxx*（n-1）+maxx就行了

AC代码：

  1 #include <cstdio>
  2 #include <algorithm>
  3 #include <iostream>
  4 #include <vector>
  5 #include <map>
  6 #include <queue>
  7 #include <set>
  8 #include <ctime>
  9 #include <cstring>
 10 #include <cstdlib>
 11 #include <math.h>
 12 using namespace std;
 13 typedef long long ll;
 14 const ll N = 2009;
 15 const ll maxn = 1e6 + 20;
 16 const ll mod = 1000000007;
 17 ll inv[maxn], vis[maxn], dis[maxn], head[maxn], dep[maxn], out[maxn];
 18 ll fac[maxn], a[maxn], b[maxn], c[maxn], pre[maxn], cnt, sizx[maxn];
 19 vector<ll> vec;
 20 char s[maxn];
 21 ll sum[maxn];
 22 ll max(ll a, ll b) { return a > b ? a : b; }
 23 ll min(ll a, ll b) { return a < b ? a : b; }
 24 ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
 25 ll lcm(ll a, ll b) { return a * b / gcd(a, b); }
 26 map<ll, ll> mp;
 27 ll ksm(ll a, ll b)
 28 {
 29     a %= mod;
 30     ll ans = 1ll;
 31     while (b)
 32     {
 33         if (b & 1)
 34             ans = (ans * a) % mod;
 35         a = (a * a) % mod;
 36         b >>= 1ll;
 37     }
 38     return ans;
 39 }
 40 ll lowbit(ll x)
 41 {
 42     return x & (-x);
 43 }
 44 ll dp[maxn][3];
 45 queue<int> q;
 46 struct node
 47 {
 48     ll v, nex;
 49 } edge[maxn << 1];
 50 void add(ll u, ll v)
 51 {
 52     edge[cnt].v = v, edge[cnt].nex = head[u];
 53     head[u] = cnt++;
 54 }
 55 void dfs1(ll u, ll fa)
 56 {
 57     dep[u] = dep[fa] + 1;
 58     sizx[u] = 1ll;
 59     for (ll i = head[u]; ~i; i = edge[i].nex)
 60     {
 61         ll v = edge[i].v;
 62         if (v != fa)
 63         {
 64             dfs1(v, u);
 65             sizx[u] += sizx[v];
 66         }
 67     }
 68 }
 69 void dfs2(ll u, ll fa)
 70 {
 71     sum[u] = sum[u] + sum[fa] + sizx[u];
 72     for (ll i = head[u]; ~i; i = edge[i].nex)
 73     {
 74         ll v = edge[i].v;
 75         if (v != fa)
 76             dfs2(v, u);
 77     }
 78 }
 79 int main()
 80 {
 81     ll t;
 82     scanf("%lld", &t);
 83     while (t--)
 84     {
 85         vec.clear();
 86         cnt = 0;
 87         ll n, m = 0, fa, k = 0, maxx = 0, ans = 0;
 88         scanf("%lld", &n);
 89         for (ll i = 0; i <= n; i++)
 90             sum[i] = out[i] = sizx[i] = dep[i] = 0, head[i] = -1;
 91         for (ll i = 2; i <= n; i++)
 92         {
 93             scanf("%lld", &fa), out[fa]++;
 94             add(fa, i), add(i, fa);
 95         }
 96         dfs1(1, 0);
 97         dfs2(1, 0);
 98         for (ll i = 1; i <= n; i++)
 99         {
100             k += sizx[i];
101             if (!out[i])
102                 vec.push_back(i);
103         }
104         m = vec.size();
105         for (ll i = 0; i < m; i++)
106         {
107             ll res = (dep[vec[i]]) * (n - 1) - sum[vec[i]] + dep[vec[i]];
108             ans = max(ans, res + k);
109         }
110         printf("%lld\n", ans);
111     }
112 }