机器学习笔记簿降维篇 LDA 01

机器学习中包含了两种相对应的学习类型：无监督学习和监督学习。无监督学习指的是让机器只从数据出发，挖掘数据本身的特性，对数据进行处理，PCA就属于无监督学习，因为它只根据数据自身来构造投影矩阵。而监督学习将使用数据和数据对应的标签，我们希望机器能够学习到数据和标签的关系，例如分类问题：机器从训练样本中学习到数据和类别标签之间的关系，使得在输入其它数据的时候，机器能够把这个数据分入正确的类别中。线性鉴别分析（Linear Discriminant Analysis, LDA）就是一个监督学习算法，它和PCA一样是降维算法，但LDA是阵对于分类问题所提出的。

1. 一个投影的LDA

设训练样本矩阵为$X=[x_1,x_2,\cdots,x_n]\in \mathbb R^{m\times n}$，其中样本向量$x_j\in\mathbb R^m(j=1,2,\cdots,n)$。假设样本被分为$c$个类，编号为$1,2,\cdots,c$，定义属于第$i$个类的样本的集合为$X_i$，第$i$个类的样本个数为$N_i$。我们首先定义第$i$个类样本的均值为

\[\mu_i=\frac{1}{N_i}\sum_{x\in X_i}x
\]

所有样本的均值为

\[\mu=\frac1n\sum_{j=1}^nx_j
\]

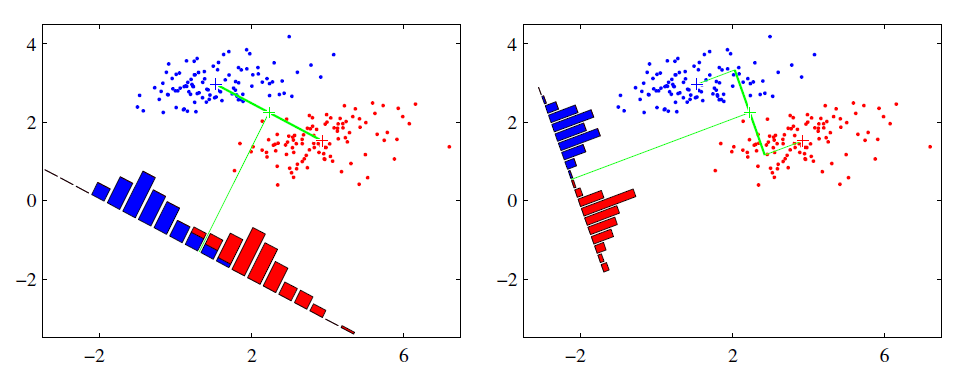
LDA的原理基于Fisher鉴别准则（Fisher Discriminant Criterion），这个准则做出了一个假设：投影后的样本集合，类间散度最大、类内散度最小，其意义在于让投影之后，类和类之间的距离尽量拉开，但是类中的个样本尽量聚集在一起，这就是LDA能够解决分类问题的精髓。设投影向量为$w\in\mathbb R^m$，那么投影后样本的类间散度可以用总均值和各个类的均值的方差来表示：

\[\begin{eqnarray*}
&&\max_{w}\sum_{i=1}^cN_i\left(w^T\mu_i-w^T\mu\right)^2\\
&=&\max_{w}\sum_{i=1}^cN_iw^T(\mu_i-\mu)(\mu_i-\mu)^Tw\\
&=&\max_{w}w^T\left[\sum_{i=1}^cN_i(\mu_i-\mu)(\mu_i-\mu)^T\right]w\tag1\\
\end{eqnarray*}\\
\]

同理，类内散度是每一个类中的样本方差之和：

\[\begin{eqnarray*}
&&\min_w\sum_{i=1}^c\sum_{x\in X_i} \left(w^Tx-w^T\mu_i\right)^2\\
&=&\min_w\sum_{i=1}^c\sum_{x\in X_i}{w^T(x-\mu_i)(x-\mu_i)^Tw}\\
&=&\min_w{w^T\left[\sum_{i=1}^c\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T\right]w}\tag{2}
\end{eqnarray*}
\]

因此，为了方便表示，我们定义类间散度矩阵$S_b$和类内散度矩阵$S_w$：

\[{
S_b=\sum_{i=1}^cN_i(\mu-\mu_i)(\mu-\mu_i)^T\\
S_w=\sum_{i=1}^c\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T
}
\]

则$(1)$和$(2)$就可以变为

\[{\max_w wS_bw\\\min_w wS_ww}
\]

LDA中通过二者相比，把它们统一成了一个优化问题：

\[\max_{w}\frac{wS_bw}{wS_ww}\tag{3}
\]

$(3)$中的目标函数是一个瑞利商（Rayleigh Quotient）（以后会有更多涉及到它的算法）的形式，这里我们先假定$S_w$是非奇异的（$S_w$是奇异的情况以后会专门讨论），这类优化问题的一般解法是变为以下形式

\[\max_{wS_ww=1}\frac{wS_bw}{wS_ww}=\max_{wS_ww=1}wS_bw\tag{4}
\]

这个变换是合理的，假设$w_0$是$(3)$中最优的投影向量，由于$S_w$非奇异（换句话说，$S_w$是正定的），则总存在一个正数$k$：

\[w_0^TS_ww_0=k>0
\]

那么总存在一个$w_*=w_0/\sqrt k$，有

\[\frac{w_0S_bw_0}{w_0S_ww_0}=\frac{w_*S_bw_*}{w_*S_ww_*},\quad w_*S_ww_*=\frac{w_0S_ww_0}{k}=1
\]

这就说明存在一个$w_*$，使得

\[w_*^TS_ww_*=1,\quad w_*=\arg\max_w\frac{wS_bw}{wS_ww}
\]

也就是说$w$的长度不对$(3)$的求解产生任何影响，因此显然$(3)$和$(4)$在这种情况下是等价的。根据$(4)$，使用拉格朗日乘数法得到：

\[S_bw=\lambda S_ww
\]

这是一个广义特征方程，由于$S_w$正定，所以$w$实际上就是$S_w^{-1}S_b$最大特征值对应的特征向量。

我们得到了$w$，就可以将样本投影到一个子空间中，即$X'=w^TX$，对于训练样本以外的未知数据$x$，如何辨认它属于哪个类呢？首先把它投影到子空间中：

\[x'=w^Tx
\]

然后采用K近邻算法（K-Nearest Neighbor, KNN），即找到离$x'_w$最近的$k$个训练样本（欧式距离），然后统计这$k$个样本都是哪个类的，不妨设这些样本的类编号为$L=[l_1,l_2,\cdots,l_k]$，最后选择$L$中的众数作为$x'$的分类结果。

KNN是一个十分简易且常用的分类算法，往往取$k=1,3,5$进行分类。由于计算高维数据的欧式距离十分耗时，因此KNN常与降维算法配合使用。当然，不只是在使用LDA时才可以使用KNN，PCA以及其它降维算法也可以配合KNN对未知样本进行分类，但PCA的分类效果一般没有LDA好（因为PCA是无监督的）。

2. 多个投影的LDA

现在我们要求的是一个投影矩阵$W\in\mathbb R^{m\times d}$，优化问题中的类间、类内散度矩阵没有变，优化问题$(3)$变为：

\[\max_{w}\frac{tr(W^TS_bW)}{tr(W^TS_wW)}\tag{5}
\]

同样当$S_w$是非奇异的时候，我们令$W^TS_wW=I$，类似的就可以得到，$W$即为$S_w^{-1}S_b$最大的$d$个特征值对应的特征向量组成。在这里我们需要注意，类间散度矩阵的秩总是不大于$c-1$，即：

\[\mathrm{rank}(S_b)\leq c-1
\]

所以$S_w^{-1}S_b$的非零特征值也最多只有$c-1$个，也就是说投影向量的个数$d$最多只能有$c-1$个，即

\[d\leq c-1
\]

因为之后得到的投影向量都将在$S_b$的零空间中，假设这个投影向量是$w'$，则$S_bw'=0$，对优化没有产生任何帮助，所以这些向量应当舍弃。也就是说LDA中，我们最多只能获取到$c-1$个有效的投影。

总结一下，LDA的步骤为：

计算类间、类内散度矩阵$S_b,S_w$
计算$S_b^{-1}S_w$的特征分解，取前$d\ (\leq c-1)$个最大特征值对应的特征向量作为投影矩阵$W$
对训练样本投影$X'=W^TX$，对于未知样本$x$也投影：$x'=W^Tx$，然后使用KNN进行分类。