poj1966 求顶点连通度

Cable TV Network

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 4563		Accepted: 2118

Description

The interconnection of the relays in a cable TV network is bi-directional. The network is connected if there is at least one interconnection path between each pair of relays present in the network. Otherwise the network is disconnected. An empty network or a network with a single relay is considered connected. The safety factor f of a network with n relays is: 
1. n, if the net remains connected regardless the number of relays removed from the net. 
2. The minimal number of relays that disconnect the network when removed. 

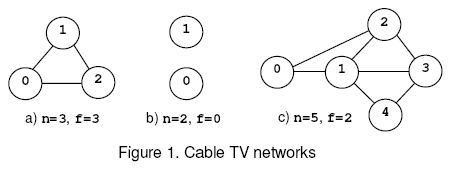
For example, consider the nets from figure 1, where the circles mark the relays and the solid lines correspond to interconnection cables. The network (a) is connected regardless the number of relays that are removed and, according to rule (1), f=n=3. The network (b) is disconnected when 0 relays are removed, hence f=0 by rule (2). The network (c) is disconnected when the relays 1 and 2 or 1 and 3 are removed. The safety factor is 2.

Input

Write a program that reads several data sets from the standard input and computes the safety factor for the cable networks encoded by the data sets. Each data set starts with two integers: 0<=n<=50,the number of relays in the net, and m, the number of cables in the net. Follow m data pairs (u,v), u < v, where u and v are relay identifiers (integers in the range 0..n-1). The pair (u,v) designates the cable that interconnects the relays u and v. The pairs may occur in any order.Except the (u,v) pairs, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.

Output

For each data set, the program prints on the standard output, from the beginning of a line, the safety factor of the encoded net.

Sample Input

0 0
1 0
3 3 (0,1) (0,2) (1,2)
2 0
5 7 (0,1) (0,2) (1,3) (1,2) (1,4) (2,3) (3,4)

Sample Output

0
1
3
0
2

 

题意：

给出n个点，m条边。求该图的连通度。

f的定义是：

1.f为n，如果不管删除多少个顶点，剩下的图仍然是连通的

2.f为删除最少的顶点数，使得剩下的图不连通

 

思路:

把点i拆成2个点i' i''，i'到i''建边，值为1。

对于原图中相连的边(u,v)，从u''连边到v'，从v''连边到u'，因为是无向图，权值为INF。

固定源点，枚举汇点，跑最大流，取最小值，如果最后的值为INF，说明是完全图，则在该题中

答案为n。否则为最大流的值。

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<string>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define INF 1<<30
#define MOD 1000000007
#define ll long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define pi acos(-1.0)
using namespace std;
const int MAXN = ;
struct node{
    int to;
    int val;
    int next;
}edge[MAXN*MAXN],edge2[MAXN*MAXN];
int pre[MAXN],vis[MAXN],ind,n,m,S,T;
void add(int x,int y,int z){
    edge2[ind].to = y;
    edge2[ind].val = z;
    edge2[ind].next = pre[x];
    pre[x] = ind ++;
}
bool bfs(int S,int T){
    memset(vis,-,sizeof(vis));
    queue<int>q;
    vis[S] = ;
    q.push(S);
    while(!q.empty()){
        int tp = q.front();
        q.pop();
        for(int i = pre[tp]; i != -; i = edge[i].next){
            int t = edge[i].to;
            if(vis[t] == - && edge[i].val){
                vis[t] = vis[tp] + ;
                q.push(t);
            }
        }
    }
    return vis[T] != -;
}
int dfs(int rt,int low){
    if(rt == T){
        return low;
    }
    int used = ;
    for(int i = pre[rt]; i != -  && used < low; i = edge[i].next){
        int t = edge[i].to;
        if(vis[t] == vis[rt] +  && edge[i].val){
            int b = dfs(t,min(low-used,edge[i].val));
            used += b;
            edge[i].val -= b;
            edge[i^].val += b;
        }
    }
    if(used == )vis[rt] = -;
    return used;
}
int dinic(int S,int T){
    int ans = ;
    while(bfs(S,T)){
        while(){
            int a = dfs(S,INF);
            if(a == )break;
            ans += a;
        }
    }
    return ans;
}
int main(){
    while(~scanf("%d%d",&n,&m)){
        if(m == ){
            if(n == )
                printf("1\n");
            else
                printf("0\n");
            continue;
        }
        ind = ;
        memset(pre,-,sizeof(pre));
        for(int i = ; i <= m; i++){
            int x,y;
            scanf(" (%d,%d)",&x,&y);
            x ++,y ++;
            add(x+n,y,INF),add(y,x+n,);
            add(y+n,x,INF),add(x,y+n,);
        }
        for(int i = ; i <= n; i++){
            add(i,i+n,),add(i+n,i,);
        }
        int ans = INF;
        for(int i = ; i <= n; i++){
            for(int j = ; j < ind; j++){
                edge[j] = edge2[j];
            }
            S =  + n,T = i;
            ans = min(ans,dinic(S,T));
        }
        if(ans == INF)ans = n;
        printf("%d\n",ans);
    }
    return ;
}