Bert不完全手册1. 推理太慢？模型蒸馏

模型蒸馏的目标主要用于模型的线上部署，解决Bert太大，推理太慢的问题。因此用一个小模型去逼近大模型的效果，实现的方式一般是Teacher-Stuent框架，先用大模型（Teacher）去对样本进行拟合，再用小模型（Student）去模仿Teacher。

为什么蒸馏本身会比直接用小模型去拟合样本取得更好的效果呢？这里先抛出几个可能的方向

• 样本降噪：大模型本身作为一个’BottleNeck‘，把难以学到的信息和噪声样本进行了一定程度过滤，降低了学习难度

• 样本增强：把大模型的预测prob作为小模型的学习目标，一定程度上其实是利用大模型对原始样本进行了数据增强，有效帮助小模型提高泛化性

• 学习目标调整：虽然小模型能力有限不能很好拟合目标，但蒸馏中核心的对齐Loss的存在使得小模型只要去模仿大模型即可，就像临摹之于绘画

知识蒸馏

说到蒸馏肯定要先提下Hinton在15年的paper，它并不是最早提出蒸馏概念的，但是它总结了几点蒸馏的方案，之后被广泛应用，主要包括以下两点

1. Temperature Softmax

\[q_i = \frac{exp(z_i/T)}{\sum_j exp(z_j/T)}
\]

想让大模型保留更高的泛化性和样本整体分布信息，可以用Temperature Softmax来smooth预测分布。Temperature就是以上的T参数，T越大模型输出的probability越平滑，置信越低。因为越复杂的模型往往越倾向于在分类问题中给出更高置信度的预测结果，以二分类为例，大模型可能会给出[0.001, 0.999]这类高置信的预测结果，而加入smooth之后会得到类似 [0.2,0.8]这类熵值更大，且更多保留了样本分布信息的预测结果。

如何理解更加smooth的分布会保留更多的样本信息？这个用多分类可能更加直观，例如在bert的MLM任务中，'天气很MASK'这时对MASK位置进行预测，高置信地预测结果可能是p(MASK=好)=0.999，而Smooth之后可能会得到P(MASK=好)=0.5，P(MASK=冷)=0.3, P(MASK=热)=0.15，很明显后者保留的文本信息更加丰富，而丰富的文本信息能进一步帮助student模型保有更好的泛化性。

1. Distill Loss

\[Loss = L_{DS} + L_{CE} = CrossEntropy(p_i, q_i)+ \alpha CrossEntropy(p_i, y_i)
\]

蒸馏的方式时让小模型同时拟合两个Loss。一个是蒸馏Loss，用相同的Temperature参数拟合以上大模型输出的soft target(\(q_i\))，其实也就是最小化student和teacher输出分布的KL散度，另一个拟合Loss是用T=1的常规softmax拟合真实的label (\(y_i\))。二者信息互为补充，大模型的soft target本身比Hard Label更容易拟合，因为大模型作为bottleNeck会过滤部分样本噪音，同时Temperature也提供了更加smooth以及容易拟合的分布信息。而HardLabel提供了熵值更低的真实信息，帮助蒸馏模型学到正确的class分类。

PKD Bert

从PKD Bert开始，大家开始集思广益对Bert开展瘦身行动。PKD在以上KD的基础上主要的创新点是在蒸馏过程中除了对输出层进行拟合之外，还加入中间层的对齐，作者称之为patient Distill，主要包括以下几个要点

1. 对哪些中间层进行对齐： 作者尝试了PKD-SKIP和PKD-LAST两种策略，对\(Bert_{12}\)来说，前者就是对[2,4,6,8,10]层进行对齐，后者就是对[7,8,9,10,11]层进行对齐。这背后主要是考虑Bert的信息分布，究竟是相对均匀的分布在各个层，还是顶层信息包含了底层信息。从效果上看是PKD- SKIP效果更好，之后的Distill 和TinyBert也都多少借鉴了这里的方案

2. 对中间层的那些信息进行对齐：这里作者只选择了对齐CLS token

3. 用什么方式进行对齐：作者用了正则化之后的CLS token Embedding之间的欧式距离来进行对齐

以上的拟合方式作者称为PT Loss，蒸馏的过程是在KD的基础上加入了PT Loss，如下

\[L_{PKD} = (1-\alpha)L_{CE} + \alpha L_{DS} + \beta L_{PT}
\]

PKD的局限性，是只针对下游任务进行蒸馏，也就是teacher模型是fine-tune Bert。并且对初始化student的方式也相对简单，直接使用了\(Bert_3\) \(Bert_6\)的预训练模型进行初始化，这里的初始化方式和以上对齐使用的PKD-Skip/LAST策略存在一定的不一致性。

Distill Bert

从DistillBert开始，蒸馏被提前到了预训练阶段。Distill Bert Base缩减了一半的层数，对比Bert Base，实现用40%更少的参数，在部分任务达到Bert97%左右的效果，比Bert预测快60%。

预训练

Distill Bert的模型结构也是6层的Transformer，在训练目标上Distill Bert使用了3个训练目标的线性组合。包括

1. \(L_{mlm}\): Mask LM Loss

student模型用和Bert相同的MLM方式直接去学习预训练任务。在后续的对比中，是否加入MLM对效果影响最小。这也印证了最初对蒸馏为何有效的讨论，蒸馏弱化了student去直接学习任务的重要性，而是更多通过模仿teacher模型去学习有效信息

1. \({L_{ce}}\): 输出层对齐

这里和KD相同，都是用了temperature softmax，除初始化之外，\(L_{ce}\)对模型效果的影响最大，所以模拟teacher输出才是distill的制胜秘籍

1. \(L_{cos}\): 隐藏层距离

Distill并没有非常强调要对内部参数进行对齐，在paper中也只是简单提及加入隐藏层之间的cosine Loss会对效果有提升

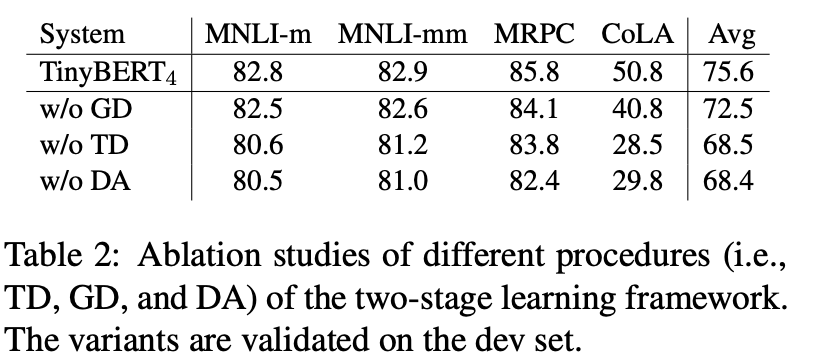
DistillBert的初始化策略借鉴了PKD-Skip，用\(Bert_{12}\)每两层取一层参数来初始化Distill，对比PKD直接用\(Bert_{6}\)的参数来初始化，这种初始化策略一致性更好。之后的预训练过程可以说是对已有参数的微调，因此初始化对整体效果的影响程度甚至超过以上3个loss function。这里其实已经能发现student和teacher能否在内部结构上保持一致对最终效果的影响很大。以下是分别去除初始化以及三种loss function对DistillBert效果影响的评估结果

下游迁移

在预训练任务上训练好的student模型，可以选择直接微调或者迁移到下游任务。不过如果再进行一次蒸馏，也就是在下游任务进行过微调的大模型上继续进行蒸馏，会得到更好的效果，在SQuad数据集上可以再有1～2个点的提升。因为小模型的拟合能力有限，所以感觉这里下游任务的复杂程度越高，进行二次蒸馏带来的效果提升会越明显。

Tiny Bert

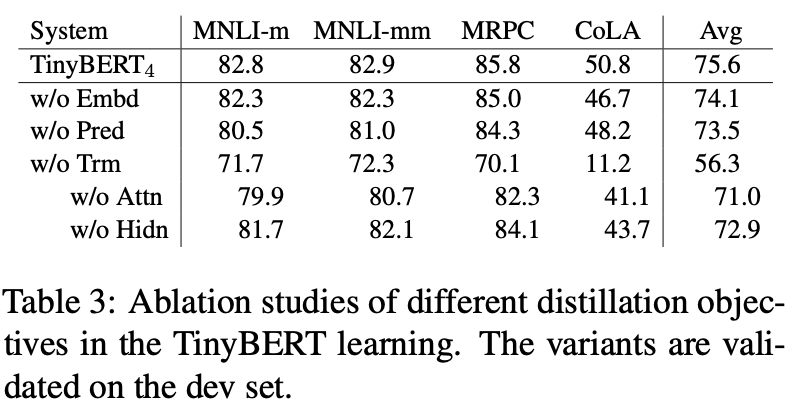
Tiny Bert在Distill的基础上完善了预训练和微调过程中蒸馏方式。作者分别给出4层和6层的两种大小，对比相同层数的DistillBert，TinyBert表现显著更好，并且进一步缩减了2/3的参数，推理速度再提升3倍

预训练

和Distill不同的是，Tiny并没有直接使用Teacher模型的参数来初始化student模型，这个差异让Tiny在参数压缩上有更大的空间。Distill只能压缩层数，而不能压缩Embedding或者Hidden Size，因为这部分是直接从Teacher初始化来的，而Tiny可以更自由的选择隐藏层的大小。

但是初始化的缺失，导致Tiny模仿Bert的难度直线上升。因此Tiny不只对隐藏层输出和输出层进行对齐，同时还加入了对Embedding和Attention矩阵的对齐。

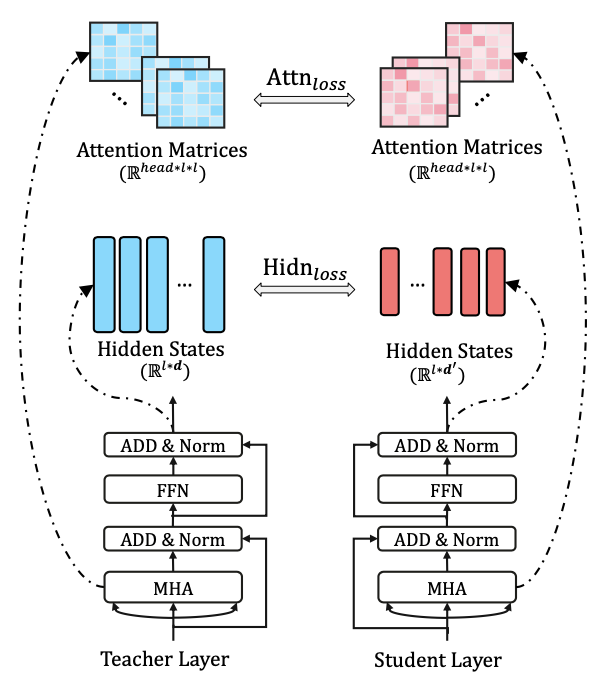
具体的Loss Function包括以下四个部分

1. \(L_{attn}\): attention矩阵对齐

有研究表明attention矩阵包含了丰富的语义语法信息，所以作者加入了未正则化的attention矩阵的对齐（对比softmax归一化后收敛更快），分别计算每个head，attention矩阵(seq_len * seq_len)之间的欧式距离

\[L_{attn} = \frac{1}{h}\sum_{i=1}^h MSE(A_i^S,A_i^T)
\]

1. \(L_{hidn}\)：隐藏层距离

这里和Distill的差异在于，Tiny允许隐藏层大小的差异，所以加入了一个线性映射\(W_h\)来对齐student和teacher隐藏层的维度。

\[L_{hidn} = MSE(H^SW_h, H^T)
\]

1. \(L_{emb}\): 输入层对齐

Tiny还加入了对输入向量的对齐，因为允许输入层的维度差异，所以也加入了对应的线性映射\(W_e\)

\[L_{emb} = MSE(E^SW_e, E^T)
\]

1. \(L_{pred}\):输出层对齐

这里和KD相同，都是用了temperature softmax，对齐student和teacher的输出层概率。

在pretrain阶段，作者评估\(L_{pred}\) 完全没有收益，因此预训练阶段只用了对齐内部参数的3个Loss，并且只train了3个epochs。个人感觉pretrain阶段只加入对齐的loss，效果类似于对大模型每个Block的hidden state进行了PCA降维，从相似的Attention信息里，只保留更重要的hidden信息输出到下一个Block。pretrain的过程只是在对齐必要的attention信息后，学习最佳的降维矩阵。所以总感觉这里好像还有进一步优化的空间，因为PCA只对hidden和emb做了，有没有可能对Attention也做个压缩？？？

在下游迁移的蒸馏中使用了以上4个loss的线性组合，在消融实验中，对模型效果的重要性影响是Atten>pred>hidden>Emb，其中Atten+hidden的效果是1+1>>2的，可见每个transformer block内部进行整体对齐是很重要的。

下游迁移

在迁移到下游任务时，Tiny选择先对中间部分（不包括\(L_{pred}\)）蒸馏10～50个epochs。因为相同的输出概率底层transformer参数分布不一定一致，但是底层transformer一致输出概率是一定一致的，所以是希望优先对齐transformer内部的参数分布。

除了蒸馏之外，TinyBert还加入数据增强。作者用预训练的Bert，以及Glove词向量来进行同义词样本增强，有P的概率，词会被GLove中的Top K同义词替换，或者会被MASK并用Bert预测得到Top K Token替换。这里作者用了P=0.4， K=15，每个原始样本生成最多20个增强样本。在日常使用中也会发现数据增强在越复杂的模型上收益越小，但是用复杂模型进行增强往往会在小模型上有更大的收益，可以更有效的提高小模型的泛化性。

在消融实验中，对迁移任务的影响是迁移蒸馏>数据增强>>预训练蒸馏，其中预训练蒸馏影响非常小，不过这里的评估数据相对有限，感觉不太能直接得出预训练蒸馏没啥用这种结论。感觉预训练的蒸馏在更复杂，样本多样性更高的任务上效果应该会更显著。毕竟对于简单任务本身Finetune对底层layer的影响就很有限，对finetune还是pretrain模型蒸馏不会有太大差异。对于Bert Finetune到底对参数有啥影响可以看下这篇博客 [博观约取系列 ～ 探测Bert Finetune对向量空间的影响](https://www.cnblogs.com/gogoSandy/p/15225813.html)

---

Reference

1. Distilling the Knowledge in a Neural Network
2. Patient Knowledge Distillation for BERT Model Compression
3. DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter
4. TinyBERT: Distilling BERT for Natural Language Understanding:
5. https://mp.weixin.qq.com/s/tKfHq49heakvjM0EVQPgHw