【数据结构&算法】05-线性表之数组

目录

• 前言
• 线性结构与非线性结构
• 数组
  • 数组的两个限制
  • 数组的随机访问特性
• 数组的操作
  • 插入操作
• 删除操作
• 数组越界
• 容器
• 数组下标

---

前言

本笔记主要记录数组的一些基础特性及操作。

顺便解答下为什么大部分编程语言的的数组是从 0 开始的。

李柱明博客：https://www.cnblogs.com/lizhuming/p/15487306.html

线性结构与非线性结构

线性结构：

• 线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。
• 包括：数组、链表、队列和栈等。

非线性结构：

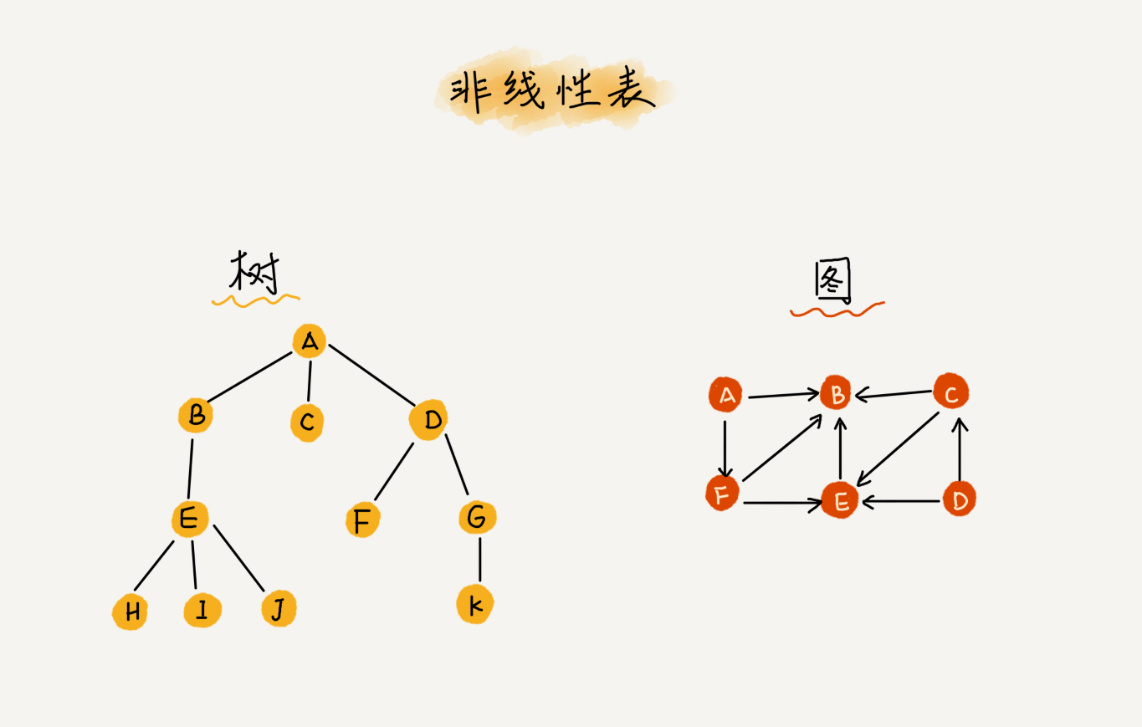
• 在非线性表，数据之间不是简单的前后关系，通过下图对比线性结构和非线性结构
• 包括：树、图等。

参考图：

数组

数组的两个限制

数组有两个限制：

1. 数组为线性结构。
2. 是连续的内存空间和相同类型的数据。

数组的随机访问特性

基于以上两个限制，使得数组具有随机访问的特性。

小笔记：

• 计算机通过地址来访问内存中的数据。

• 寻址通过以下公式寻址：

  a[i]_address = base_address + i * data_type_size;
  

而随机访问是只要知道数组对应的下标，我们就可以直接通过寻址公式知道该数据，不需要查找什么的。使得时间复杂度为 O(1)。

小笔记：

• 数组和链表的区别：

  • 数组支持随机访问，根据下标随机访问的时间复杂度为 O(1)。
  • 链表适合增删，时间复杂度为 O(1)。

数组的操作

数组的操作主要是增删。

插入操作

插入数据，若不是尾部且不能留空，则需要搬移部分数据。

分析：

• 若插入尾部，则不需要搬移数据，插入操作的时间复杂度为 O(1)。

• 若插入第 k 个位置中。其插入操作的时间复杂度为 O(n)。

  • 特定情况下，可以把原有第 k 个位置中的数据挪到最后。这样其插入操作的时间复杂度为 O(1)。

删除操作

删除数据，若不是尾部且不能留空，则需要搬移部分数据。

分析：

• 若删除尾部，则不需要搬移数据，删除操作的时间复杂度为 O(1)。

• 若删除第 k 个位置中。其删除操作的时间复杂度为 O(n)。

  • 特定情况下，若删除的位前面几个，则可以直接修改数组的起始位置即可。

数组越界

小笔记：一个由 C/C++ 编译的程序占用的内存分为以下几个部分：

• 堆区（stack）：

  • 生长开口方向向上。（底为低地址、小端）
  • 一般由程序员分配释放， 若程序员不释放，程序结束时可能
    由 OS 回收 。

• 栈区（heap）：

  • 生长开口方向向下。（底为低地址、小端）
  • 由编译器自动分配释放 ，存放函数的参数值，局部变量的值
    等。其操作方式类似于数据结构中的栈。

• 全局区（静态区）（static）：

  • 全局变量和静态变量的存储是放在一块的，初始化的全局变量和静态变量在一块区域， 未初始化的全局变量和未初始化的静态变量在相邻的另一块区域。
  • 程序结束后有系统释放

• 文字常量区：

  • 常量字符串就是放在这里的。
  • 程序结束后由系统释放。

• 程序代码区：

  • 存放函数体的二进制代码。

参考代码：

int main(int argc, char* argv[])
{
    int i = 0;
    int arr[3] = {0};

    for(; i<=3; i++)
    {
        arr[i] = 0;
        printf("hello world\n");
    }
    return 0;
}

分析：

• 该代码无限打印 hello world\n 。就是因为内存溢出。
• 整型变量 i 和整型数组 arr[3] 存储在栈空间中。
• arr[3] 的存储位置就是 i 的存储位置。
• for 循环的合法循环 i 最大为 3，刚好在 i=3 的那次循环把 i 重置为 0 了。

这种数组越界的错误容易导致逻辑混乱。程序跑飞。

容器

针对数组类型，很多语言都提供了容器类，比如 Java 中的 ArrayList、C++ STL 中的 vector。

容器把很多数组操作的细节封装起来，如插入、删除等，且支持扩容。

数组下标

为什么大多数编程语言中，数组要从 0 开始编号，而不是从 1 开始呢？

• 寻址效率原因。
• 历史原因。

寻址：

• 正常寻址：

  a[k]_address = base_address + k * type_size;
  

• 若数组下标起始为 1 的寻址：

  a[k]_address = base_address + (k-1)*type_size;
  

每次寻址多了一个减法指令。

历史：

• C 语言设计者用 0 开始计数数组下标，之后的 Java、JavaScript 等高级语言都效仿了 C 语言。

小笔记：

• python 支持负下标。