聚类算法K-Means算法和Mean Shift算法介绍及实现

Question:什么是聚类算法

1、聚类算法是一种非监督学习算法

2、聚类是在没有给定划分类别的情况下，根据数据相似度进行样本分组的一种方法

3、理论上，相同的组的数据之间有相同的属性或者是特征，不同组数据之间的属性或者特征1相差就会比较大

聚类算法分类：

1、划分方法（k-means)

划分方法通过优化一个划分标准的方式将数据集D组织成k个簇

2、层次方法（sahn)

层次方法在不同粒度水平上为数据集D创造层次聚类，其中每层特定的聚类结果由相应粒度水平的阈值决定

3、基于密度的方法（Mean Shift)

基于密度的方法从密度的角度构造簇类

4、基于网格的方法（STING)

基于网格的方法是将数据集D量化进数量有限的网格单元中，量化过程通常是多分辨率的

5、基于模型的方法（GMM)

假设存在一个数学模型能够对数据集D的性质进行描述，通过对数据和该模型的符合程度进行优化，可以得到优化的结果

K-Means算法

1、核心思想K-Means聚类算法也称K均值聚类算法，它采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度也越大。

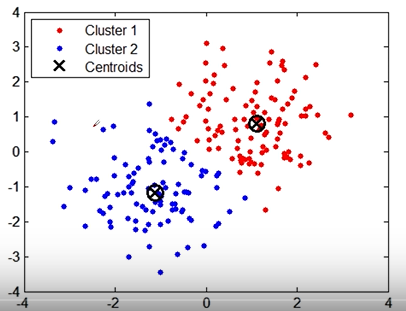
2、算法实现

1）首先确定一个K值，即我们希望将数据集经过聚类得到K个集合

2）将数据集中随机选择K个数据点作为质心

3）对数据集中每个点，计算其与每一个质心的距离（如欧式距离），离哪个质心近，就划到哪个质心所属的集合

4）把所有数据归好集合后，一共有k个集合，然后重新计算每个集合的质心（数据均值）

5）如果新计算出来的质心和原来的质心的距离小于某一个设置的阈值，我们可以认为聚类已经达到期望的结果，算法终止

6）如果新质心和原质心距离变化很大，需要迭代3-5步骤

2、Mean Shift算法