N皇后演示程序

问题描述:

在N×N格的棋盘上放置彼此不受攻击的N个皇后，按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子，求解可以放置的布局方式。

设计要求：

(1) 要求实现图形化棋盘显示；

(2) 要求实现N皇后布局演示，可以使用方向键进行布局切换。

问题分析:

当n的个数比较小时，我们可以采用穷举法来列举可能出现的情况，但当n的个数比较大时，就需要考虑其他的方法了。在n*n的棋盘上，每个皇后可能有n个摆放位置，有两种方法可以来进行判断:

1.最后一个皇后已经放到棋盘，此时在进行判断是否满足条件。

2.每放一个皇后就进行判断，当不满足条件时，后面的情况就不用再考虑了，直接看下一个摆放的位置。

如下图:

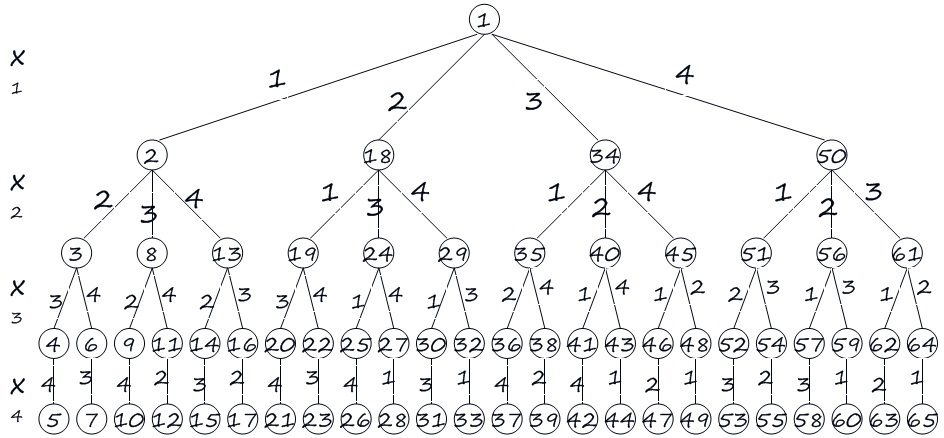
因此我们就可以得到解题思路，每放一个皇后就与上一个进行判断，判断该位置是否与前面的皇后发生冲突。

算法实现:

#include<cmath>
using namespace std;
int n,tol=0; // N皇后个数和成功个数
int queen[100] = {0};  //[]里的值代表行数,value值代表列数
int col[1000][100] = {0};  //用来存放成功的数据
bool check(int r,int c){ // (r,c)代表新皇后的坐标
    for(int i=0;i<r;i++){
        if(queen[i]==c||(abs(queen[i]-c) == abs(r-i))){ // 判断是否冲突(第一个判断的是行数等于列数，即对角线)
            return false;
        }
    }
    return true;
}
void DFS(int r){
    if(r==n){ //判断最后一个是否已经放到棋盘,最后一个放到棋盘，说明是一种解法
        for(int i=0;i<n;i++){
            col[tol][i] = queen[i]; //讲棋盘存到总的期盼里
        }
        tol++; //成功次数++
        //queen[100]={}; //初始临时棋盘
        return;
    }

    for(int c=0;c<n;c++){
        if(check(r,c)){  //判断该位置是否与前n-1个位置冲突
            queen[r] = c; //不冲突赋值
            DFS(r+1); //进行一下行操作
        }
    }
}
void show(int r){
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            if(col[r][i]==j){//col[r][i]有保存的值，和j做比较
                cout<<"Q   ";
            }else{
                cout<<"X   ";
            }
        }
        cout<<endl<<endl;
    }
    cout<<"************当前页数"<<r+1<<"************"<<endl<<endl;
    cout<<"*********->查看下一个,<-查看上一个*********"<<endl;
}
int main(){
    cout<<"请输入皇后的数量:";
    cin>>n;
    if(n<3){
        cout<<"无解！"<<endl;
        return 0;
    }
    DFS(0);
    cout<<"一共有"<<tol<<"种布局"<<endl<<endl;
    int ch1=0;
    int ch2=0;
    int current = 0;
    show(current);
    //实现左右翻页
    while (1){   //无限循环
        //使用getch()读取方向键,读取方向键需要读取两次
          if (ch1=getch()){
             ch2=getch();//第一次调用getch()，返回值224
             switch (ch2){//第二次调用getch()
             case 75: {  //←的ascll
                 if(current-1>=0){
                    current--;
                 }else{
                     current = tol-1;
                 }
                    system("cls\n");
                    cout<<"请输入皇后的数量:"<<n<<endl;
                    cout<<"一共有"<<tol<<"种布局"<<endl<<endl;
                    show(current);
                break;
             }
             case 77: {
                 if(current+1<=tol-1){
                    current++;
                 }else{
                     current = 0;
                 }
                    system("cls\n");
                    cout<<"请输入皇后的数量:"<<n<<endl;
                    cout<<"一共有"<<tol<<"种布局"<<endl<<endl;
                    show(current);

                 break;
             }
             default:cout<<"输入错误！"<<endl;break;

             }
          }
        }
       return 0;
}

代码说明:

采用数组来存放结果，方向键的切换是采用读取getch来实现的。在函数check()中，判断冲突的条件是通过循环遍历来检验刚刚放进的第r行皇后是否与前r-1行放的发生冲突，即行数相等或列数相等。

资料参考:

n皇后详解及代码实现/C++ - Geek_Ling - 博客园 (cnblogs.com)

https://www.cnblogs.com/yangxiao-/p/13683675.html