特征向量、特征值以及降维方法（PCA、SVD、LDA）

一、特征向量/特征值

　　Av = λv

　　如果把矩阵看作是一个运动，运动的方向叫做特征向量，运动的速度叫做特征值。对于上式，v为A矩阵的特征向量，λ为A矩阵的特征值。

　　假设：v不是A的速度（方向）

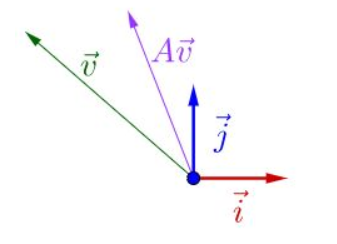
　　结果如上，不能满足上式的。

二、协方差矩阵

　　方差（Variance）是度量一组数据分散的程度。方差是各个样本与样本均值的差的平方和的均值。

　　协方差（Covariance）是度量两个变量的变动的同步程度，也就是度量两个变量线性相关性程度。如果两个变量的协方差为0，则统计学上认为二者线性无关。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

三、主成分分析法（PCA）

　　特征降维一般有两类方法：特征选择和特征抽取。特征选择即从高纬度的特征中选择其中的一个子集来作为新的特征；而特征抽取是指将高纬度的特征经过某个函数映射至低纬度作为新的特征。常用的特征抽取方法就是PCA。主成分分析法（PCA）是常用的一种降维方法。对于正交属性空间中的样本点，如何用一个超平面对所有的样本进行恰当的表达？

　　　　1、最近重构性，样本到这个超平面的距离都足够近

　　　　2、最大可分性，样本点到这个超平面上的投影能尽可能分开

　　首先：假设数据样本进行了中心化（对所有样本进行中心化，对每个维度减去这个维度的数据均值），假设投影变换得到的新坐标系为{w1,w2,...,wi},W为标准正交向量基，||wi||2=1,w_i^Tw_j=0(i!=j)，对于样本点x_i到超频面的投影为W^Tx_i,若所有样本点的投影尽可能分开，则投影后的样本点方差应该最大。

　　投影后的方差：∑W^Tx_ix_i^TW，于是目标函数为：

　　max  W^TXX^TW       s.t. W^TW=I

　　等价 min （-max）

　　采用拉格朗日乘子法：

　　F = -W^TXX^TW +λ（I-W^TW）

　　∂F/∂W = 0  推导出：

　　XX^Tw_i = λ_iw_i

　　此时，只要对协方差XX^T 进行特征值分解，求得特征值以及特征向量的排序，λ₁ ≥λ₂  ....  λ_i，对应的W的排序就为主成分分析的解。

　　实际上，PCA主成分分析的求解或者说解释是通过拉格朗日乘子法进行推到的，只不过求解结果可以通过求解特征值的形式进行求解。而从特征值的角度来看，特征值和特征向量反映了协方差的变化规律。

 四、PCA流程

• 对数据去中心化
• 计算XX^T，注:这里除或不除样本数量M或M−1其实对求出的特征向量没影响
• 对XX^T进行特征分解
• 选取特征值最大的几个维度进行数据映射。（去掉较小的维度）

　　下面，可以通过代码看PCA降维如何操作的：

import numpy as np
from sklearn.decomposition import PCA
#零均值化
def zeroMean(dataMat):
    meanVal=np.mean(dataMat,axis=0)     #按列求均值，即求各个特征的均值
    newData=dataMat-meanVal
    return newData,meanVal

def pca(dataMat,n):
    newData,meanVal=zeroMean(dataMat)
    covMat=np.cov(newData,rowvar=0)    #求协方差矩阵,return ndarray；若rowvar非0，一列代表一个样本，为0，一行代表一个样本

    eigVals,eigVects=np.linalg.eig(np.mat(covMat))#求特征值和特征向量,特征向量是按列放的，即一列代表一个特征向量
    #print(eigVals)
    #argsort将x中的元素从小到大排列，提取其对应的index(索引)
    eigValIndice=np.argsort(eigVals)            #对特征值从小到大排序
    #print(eigValIndice)
    n_eigValIndice=eigValIndice[-1:-(n+1):-1]   #最大的n个特征值的下标
    n_eigVect=eigVects[:,n_eigValIndice]        #最大的n个特征值对应的特征向量
    lowDDataMat=newData*n_eigVect               #低维特征空间的数据
    reconMat=(lowDDataMat*n_eigVect.T)+meanVal  #重构数据
    return lowDDataMat,reconMat

dataMat = np.array([i for i in range(100)]).reshape(10,10)

data ,mat = pca(dataMat,2)
print(data)
p = PCA(n_components=2)
main_vector = p.fit_transform(dataMat)
print(main_vector)

　　如上，可以看到PCA的实现过程，但是我们自己实现的PCA的结果和sklearn实现的结果不一样，是因为sklearn中的PCA实际上是通过SVD实现的。

五、奇异值分解（SVD）

　　奇异值分解是一种重要的矩阵分解方法。

　　假设A是一个mxn的矩阵，则存在一个分解使得

　　A_mn = U_mm∑_mnV_nn^T

　　与特征值、特征向量概念相对应，则：

　　∑对角线上的元素成为矩阵A的奇异值，U和V称为A的左右奇异向量矩阵。

　　左奇异向量用于压缩行，右奇异向量压缩列。压缩方法均是取奇异值较大的左奇异向量或者右奇异向量与原数据C相乘。

　　PCA是从特征方向去降维，而SVD从特征和实例两个方向降维。

　　SVD计算过程：假设原数据为X，一行代表一个样本，列代表特征。

　　　　1）计算X'X，XX'；

　　　　2）对XX'进行特征值分解，得到的特征向量组成u，lambda_u;

　　　　3）对X'X进行特征值分解，得到的特征向量组成v，lambda_v;

　　　　4）lambda_u，lambda_v的重复元素开方组成对角矩阵sigma主对角线上的元素；

六、LDA降维方法

　　LDA（线性判别分析）是一种基于分类模型进行特征属性合并的操作，是一种有监督的降维方法。 在sklearn中本质就是SVD分解的左奇异矩阵乘以原来的矩阵，达到降实例的目的。该过程可以通过k-means同样实现。

　　LDA用于分类问题：

import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
y = np.array([1, 1, 1, 2, 2, 2])
clf = LinearDiscriminantAnalysis()
clf.fit(X, y)
print(clf.predict([[-0.8, -1]]))

　　

　　LDA用于降维：

lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X,y)
X_new = lda.transform(X)

　　

七、PCA与LDA对比以及应用场景

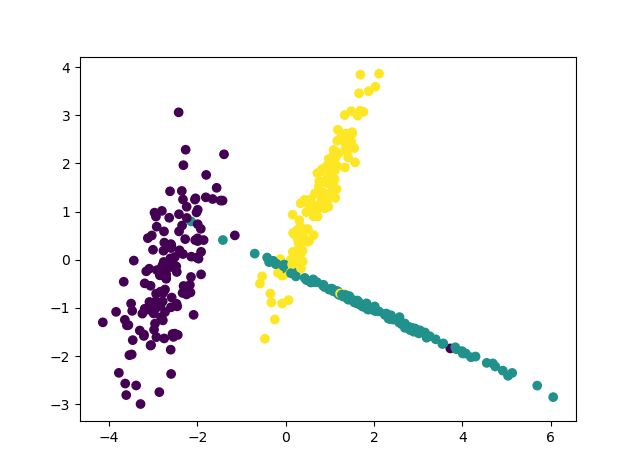
　　PCA与LDA效果对比可以参考：http://scikit-learn.org/stable/auto_examples/decomposition/plot_pca_vs_lda.html#sphx-glr-auto-examples-decomposition-plot-pca-vs-lda-py

　　

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets.samples_generator import make_classification
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# X1为样本特征，Y1为样本类别输出， 共400个样本，每个样本3个特征，输出有3个类别，没有冗余特征，每个类别一个簇
X, Y = make_classification(n_samples=400, n_features=3, n_redundant=0,
                             n_clusters_per_class=1, n_classes=3,random_state = 7)
fig = plt.figure()
ax = Axes3D(fig)
plt.scatter(X[:, 0], X[:, 1], X[:, 2],linewidths=5,marker='o',c=Y)
plt.show()

# PCA降维
pca = PCA(n_components=2)
pca.fit(X)
X_new = pca.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1],marker='o',c=Y)
plt.show()

#LDA降维
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X,Y)
X_new = lda.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1],marker='o',c=Y)
plt.show()

　　

PCA

LDA

　　PCA映射是一种将高维数据合并到低维的过程，样本具有更大的发散性；LDA考虑了样本的标注，即希望投影后，不同类别之间的距离最大，可以用于降维和分类。

• 　　一般情况下，有类别信息时，可以采用LDA
• 　　无类别信息，不知道样本属于哪个类，用PCA