Dijkstra(迪杰斯特拉)算法求解最短路径

过程

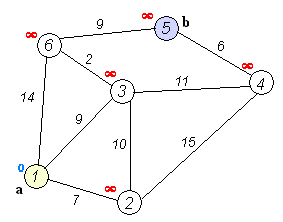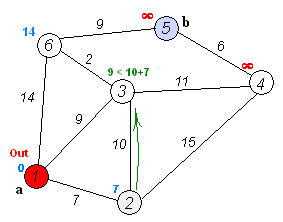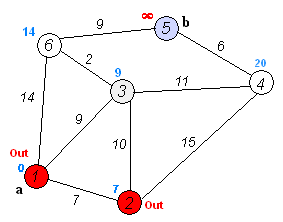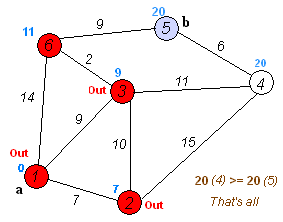
首先需要记录每个点到原点的距离，这个距离会在每一轮遍历的过程中刷新。每一个节点到原点的最短路径是其上一个节点（前驱节点）到原点的最短路径加上前驱节点到该节点的距离。以这个原则，经过N轮计算就能得到每一个节点的最短距离。

第一轮，可以计算出，2、3、4、5、6到原点1的距离分别为：[7, 9, -1, -1, 14]。-1表示无穷大。取其中最小的，为7，即可以确定1的最短路径为0，2为下一轮的前驱节点。同时确定2节点的最短路径为7，路线：1->2。

第二轮，取2节点为前驱节点，按照前驱节点的最短距离加上该节点与前驱节点的距离计算新的最短距离，可以得到3，4，5，6节点到原点的距离为：[17, 22, -1, -1]，此时需要将这一轮得到的结果与上一轮的比较，3节点：17 > 9，最短路径仍然为9；4节点：22 < 无穷大，刷新4节点的最短路径为22；5节点：不变，仍然为无穷大；6节点：14 < 无穷大，取14，不变。则可以得到本轮的最短距离为：[9, 22, -1, 14]，取最短路径最小的节点，为3，作为下一轮的前驱节点。同时确定3节点的最短路径为9，路线：1->3。

第三轮，同上，以3为前驱节点，得到4，5，6的计算距离为：[20, -1, 11]，按照取最短路径的原则，与上一轮的进行比较，刷新为：[20, –1, 11]，选定6为下一轮的前驱节点。同时取定6的最短路径为11，路线：1->3->6。

第四轮，同上，以6为前驱节点，得到4和5的计算距离为[20, 20]，与上一轮进行比较，刷新后为[20, 20]，二者相等只剩下两个节点，并且二者想等，剩下的计算已经不需要了。则两个节点的最短路径都为20。整个计算结束。4的最短路径为20，路线：1->3->4。5的最短路径为20，路线：1->3->6->5。

如果二者不相等，则还需要进行第五轮，先确定二者中的一个的最短路径和路线，再取定剩下的。直到整个5次循环都完成。

伪代码

function Dijkstra(G, w, s)
   for each vertex v in V[G]         //初始化
         d[v] := infinity             //将各点的已知最短距离先设成无穷大
         previous[v] := undefined     // 各点的已知最短路径上的前趋都未知
   d[s] := 0                         // 因为出发点到出发点间不需移动任何距离，所以可以直接将s到s的最小距离设为0
   S := empty set
   Q := set of all vertices
   while Q is not an empty set       // Dijkstra算法主体
         u := Extract_Min(Q)
         S.append(u)
         for each edge outgoing from u as (u,v)
                if d[v] > d[u] + w(u,v)       // 拓展边（u,v）。w(u,v)为从u到v的路径长度。
                      d[v] := d[u] + w(u,v)   // 更新路径长度到更小的那个和值。
                      previous[v] := u        // 记录前面顶点

Code

public class Dijkstra
{
    public static final int M = -1;

    public static void main(String[] args)
    {
        int[][] map1 = {
                { 0,  7,  9,  M,  M, 14 },
                { 7,  0,  10, 15, M, M },
                { 9,  10, 0,  11, M, 2 },
                { M,  15, 11, 0,  6, M },
                { M,  M,  M,  6,  0, 9 },
                { 14, M,  2,  M,  9, 0 } };

        int orig = 0;
        int[] shortPath = Dijsktra(map1, orig);

        if (shortPath == null)
        {
            return;
        }

        for (int i = 0; i < shortPath.length; i++)
        {
            System.out.println("从" + (orig + 1) + "出发到" + (i + 1) + "的最短距离为："
                    + shortPath[i]);
        }
    }

    public static int[] Dijsktra(int[][] weight, int orig)
    {
        int n = weight.length;              // 顶点个数

        int[] shortest = new int[n];        // 存放从start到其他各点的最短路径
        boolean[] visited = new boolean[n]; // 标记当前该顶点的最短路径是否已经求出，true表示已求出

        // 初始化，第一个顶点求出
        shortest[orig] = 0;
        visited[orig] = true;

        for (int count = 0; count != n - 1; count++) // 要加入n-1个顶点
        {
            // 选出一个距离初始顶点最近的未标记顶点
            int k = M;
            int dmin = M;
            for (int i = 0; i < n; i++)
            {
                if (!visited[i] && weight[orig][i] != M)
                {
                     if (dmin == -1 || dmin > weight[orig][i])
                     {
                         dmin = weight[orig][i];
                         k = i;
                     }
                }
            }

            // 正确的图生成的矩阵不可能出现K == M的情况
            if (k == M)
            {
                System.out.println("the input map matrix is wrong!");
                return null;
            }

            shortest[k] = dmin;
            visited[k] = true;

            // 以k为中间点，修正从原点到未访问各点的距离
            for (int i = 0; i < n; i++)
            {
                if (!visited[i] && weight[k][i] != M)
                {
                    int callen = dmin + weight[k][i];
                    if (weight[orig][i] == M || weight[orig][i] > callen)
                    {
                        weight[orig][i] = callen;
                    }
                }
            }
        }

        return shortest;
    }
}

我是天王盖地虎的分割线

参考：http://codeway.co/dijkstra%E7%AE%97%E6%B3%95%E6%B1%82%E8%A7%A3%E6%9C%80%E7%9F%AD%E8%B7%AF%E5%BE%84%E5%88%86%E6%9E%90/