线性代数的视角理解LSR(least square regression)的参数评估算法本质

https://medium.com/@andrew.chamberlain/the-linear-algebra-view-of-least-squares-regression-f67044b7f39b

线性回归是初学者学习的最重要的统计模型工具。然而，传统的教学方式使得我们很难理解到这个regression的本质。大多数课程聚焦在"计算"视图上，在这个计算视图中，regression关注于每个观察值和预测值之间差的平方和所形成的表达式，随后我们对这个表达式应用求导取0，最终算得各个系数的值。

大多数教科书诱导学生们关注在这个痛苦的计算过程上，随后依赖于类似R或者Stata的统计软件包上，这导致学生严重依赖于这些软件，而不会深入理解到底是怎么工作的，其本质是什么。。这往往是不真正理解数学的老师去教regression的常见方式。

在本文中，我将更优雅简单地演示LSR的本质，我把他称为"线性代数"视图。

问题导入

regression的终极目标是找到一个合适的model来拟合一系列观测值的集合。本例中，我搜集了一些工厂每天机器故障的次数，比如我已经获取了三个数据点(day, number of failure): (1,1),(2,2),(3,2)。

我们的目标是寻找到一个线性方程来拟合这三个点。我们相信存在一个数学映射，将"days"唯一映射为"failures"，或者说:

以 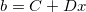的形式来映射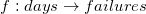

这里b就是每天的机器故障数, x是day, C,D是线性变换的系数，这也是我们要寻找的未知数。

我们将已知的三个数据点代入线性方程，得到:

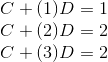
对于前两个点，model fit的非常好，但是第三个点却开始出现问题，也就是说我们已经意识到：这三个点并不在一条直线上，我们的model只能最大限度的近似它。

我们来看看如何以$Ax = b$的方式来表达我们的线性模型：

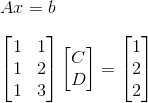
从这个矩阵中，我们可以说我们希望向量$\vec{b}$存在于矩阵$A$的列空间$C(A)$中.也就是说，我们希望通过矩阵A的列向量做线性组合能够得到我们的观测值$b$列向量。

然而，不幸的是，我们已经知道$b$本身并不能完全由A的列向量线性表示。这意味着向量$b$并不在$A$的列空间中.所以我们并不能通过解线性方程组的方式来求解到$x(C,D)$.

我们来继续通过画图来了解发生着什么。

在下面的手绘中，矩阵A的列向量空间被记为$C(A)$。它为三维空间中的一个平面。如果我们将矩阵$A$的两个列向量记录为$a_1,a_2$，则列空间就是两个列向量所有线性组合构成的平面。

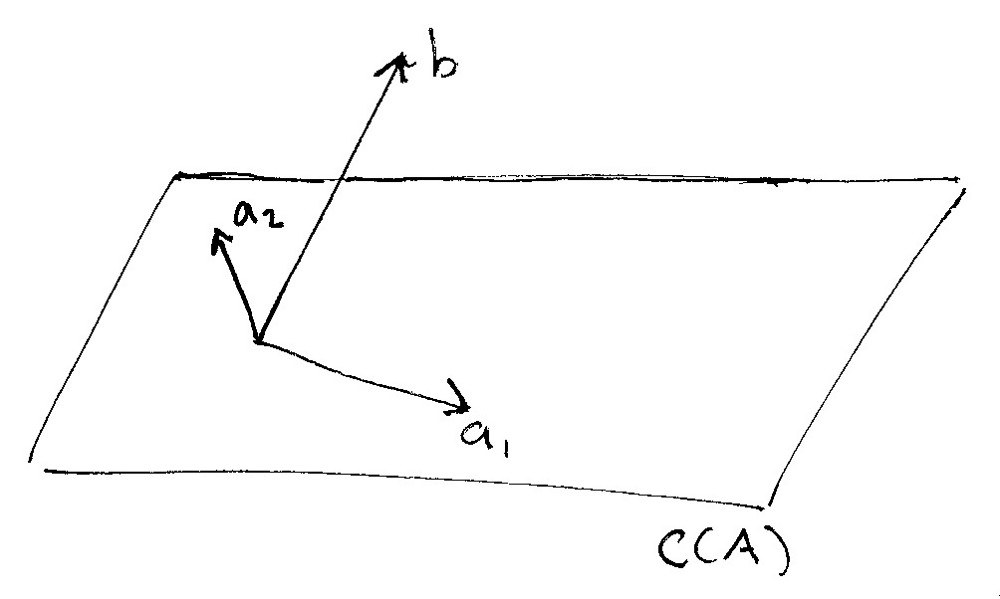
同时你可以看到观测值构成的列向量$b$并不存在于该平面中，而是和该平面有所交集，被标志为$b$。

平面$C(A)$是我们理想的数学模型，而向量$b$则是我们实际的观测值向量，并不能完美地落在线性空间$C(A)$中，那么我们需要怎么去做呢？

线性回归模型的方法是：我们应该放弃寻找一个model能够完美拟合到$b$，相反的是我们应该找到一个另外一个足够接近目标$b$向量的向量，而该向量能够在$A$的列空间中。也就是说我们需要在列空间中找到一个向量$p$，使得$p$和$a$越靠近越好。

下面的图片演示了这个过程。我们可以想象一下，如果从$C(A)$平面的正上方向下打一个光线，这将在$C(A)$上形成一个线段的影子。这实际上就是向量$b$在矩阵$A$的列空间平面上的投影projection.这个投影在图中我们以$p$标签来标识。

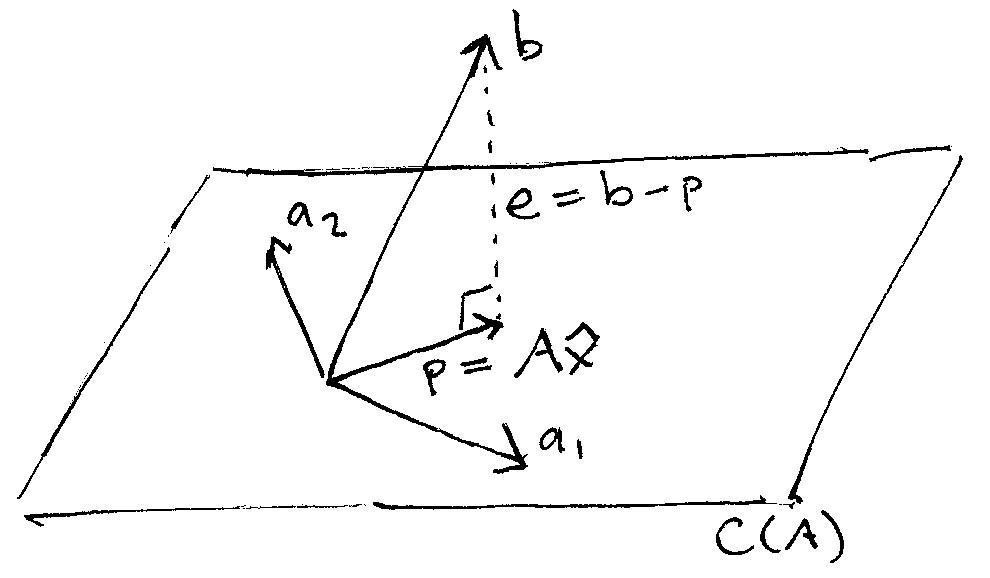
被标注为$e$的向量实际上是真值向量$b$和我们计划使用的投影向量$p(\hat{b})$之间的。现在我们可以将我们的目标使用另外一种方式来描述:寻找一个合适的向量$p$使得$e$越小越好。也就是说，我们希望最小化$p,b$之间的误差。

在上面的图中，$e$就是观察值向量$b$减去投影向量$p$或者记为$b-p$.而投影向量$p$本身就是$A$的列向量线性组合----这也是为什么$p$能够在$A$的列空间中的原因----所以$p$应该等于$A$去乘以一个向量，我们记为$\hat{x}$

为了最小化这个$e$，我们希望选择一个垂直于$e$但和$b$同向的向量$p$，在图中，$e$和$p$的夹角我们标注为90度的角。

求解Regression系数

既然e和A的列空间平面垂直，那么意味着$A$的列向量和$e$的点乘都为0(因为列空间的所有向量都和$e$垂直，而$A$的列向量必然在列空间里，故而)，$A\cdot e = 0,A^T\times e = 0$, 同时既然$e=b-p, p = A \times \hat{x}$，我们就可以得到:

$$A^{T}(b-A\hat{x})=0$$

从上面方程中解出$\hat{x}$,我们就得到:

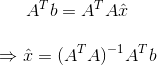
$\hat{x}$的每个元素就是计算出来的系数$C,D$,这正是我们要寻找的。做线性回归本质上就是在解方程:$Ax = b$,但是如果任何b中的观测值背离线性模型，那么A将不是可逆矩阵。因此我们通过在左右分别乘上矩阵$A$的转置矩阵$A^{T}$使得其为可逆矩阵。$A^{T}A$总是一个对称的方阵，所以是可逆的，然后我们就用它来求解$\hat{x}$

使用这种代数视图还有其他的一些好处，其中之一：非常方便理解相关系数$r$.如果我們正規化x,y数据点，也就是说分别减去其均值，那么r就是$b,C(A)$的夹角的余弦值。

$cos()$函数值的范围是-1到1，就和r的值域一样。如果regression完全拟合，r=1,这意味着$b$在平面上。如果b在平面上，那么夹角是0，而$cos(0)=1$,相反，如果regression非常糟糕，r=0,而b和平面是垂直的，这时$cos(pi/2)=0$