[csp-201809-4]再卖菜 差分约束or记忆化搜索

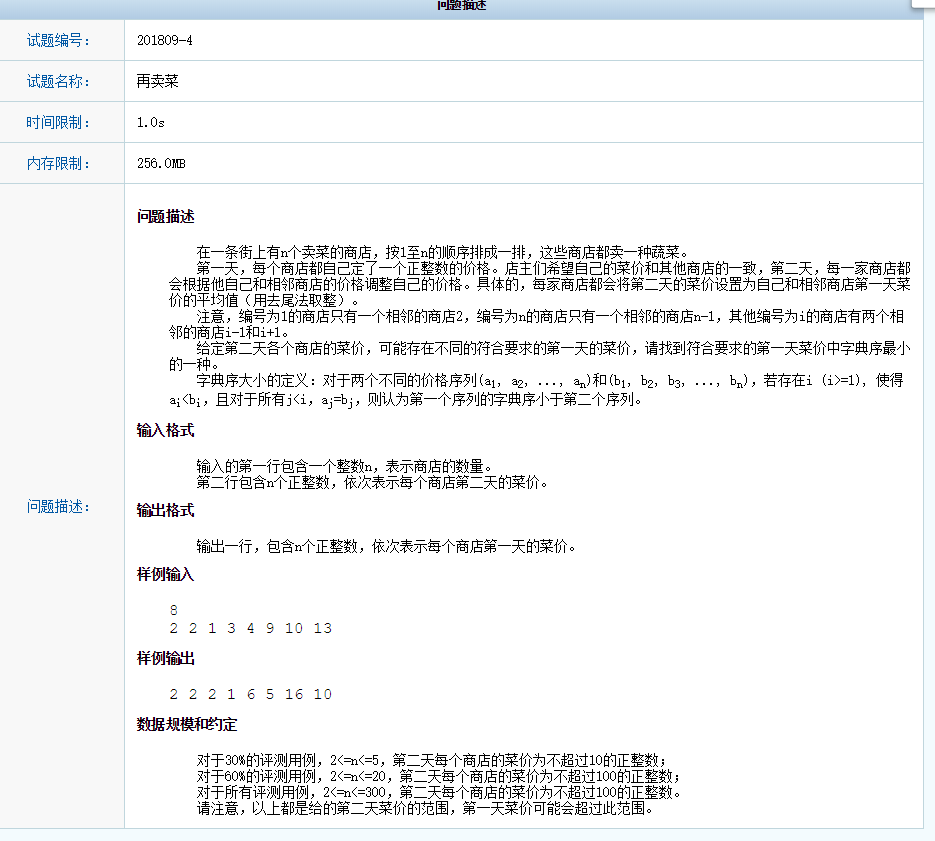
先更新第一个做法：差分约束

转化成最长路，求出的每一个解是满足差分方程的最小值

spfa求最短路

对于边(x->y) 有：

if(dis[y] > dis[x] + a[i].d) dis[y]=dis[x]+a[i].d;

dis[y]的初始值为INF，dis[y]会是满足所有约束条件之中所有可能的值之中最大的（更新到最大的就不会再更新了）。

贴一个简略的证明：

同理，最长路求出来的是所有可能解之中最大的。

这题是字典序最小，那么我们要转化成最长路来求，求到的每个s[i]都是可能的值中最小的一个。注意，菜价要是正整数(>=1)。

 #include<bits/stdc++.h>
 using namespace std;

 const int N=;
 struct node{
     int x,y,d,next;
 }a[*N];
 int n,al,first[N],b[N],s[N];
 bool vis[N];
 queue<int> q;

 void ins(int x,int y,int d)
 {
     al++;
     a[al].x=x;a[al].y=y;a[al].d=d;
     a[al].next=first[x];first[x]=al;
 }

 void build_edge()
 {
     al=;
     memset(first,,sizeof(first));
     ins(,,*b[]);
     ins(,,-(*b[]+));
     for(int i=;i<=n-;i++)
     {
         ins(i-,i+,*b[i]);
         ins(i+,i-,-(*b[i]+));
     }
     ins(n-,n,*b[n]);
     ins(n,n-,-(*b[n]+));
     for(int i=;i<=n;i++) ins(i-,i,);
 }

 void spfa()
 {
     while(!q.empty()) q.pop();
     memset(s,,sizeof(s));
     memset(vis,,sizeof(vis));
     s[]=;vis[]=;q.push();
     while(!q.empty())
     {
         int x=q.front();q.pop();
         for(int i=first[x];i;i=a[i].next)
         {
             int y=a[i].y;
             if(s[y]<s[x]+a[i].d)
             {
                 s[y]=s[x]+a[i].d;
                 if(!vis[y])
                 {
                     vis[y]=;
                     q.push(y);
                 }
             }
         }
         vis[x]=;
     }
 }

 int main()
 {
     //freopen("a.in","r",stdin);
     scanf("%d",&n);
     for(int i=;i<=n;i++) scanf("%d",&b[i]);
     build_edge();
     spfa();
     for(int i=;i<=n;i++)
         printf("%d ",s[i]-s[i-]);printf("\n");
     return ;
 }