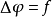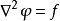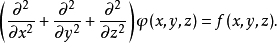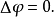Poisson Blending(Seamless clone)研究和实现

 是S的一个封闭子集,它的边界为
是S的一个封闭子集,它的边界为 。令f*为定义在S上一个已知的标量函数,代表S减去
。令f*为定义在S上一个已知的标量函数,代表S减去 的范围,令f为定义在
的范围,令f为定义在 上一个未知的标量函数。最终,令v为定义在
上一个未知的标量函数。最终,令v为定义在 上的向量域。
上的向量域。定义在 上f*的最简单的插值函数f:最小化问题的插值(在边界是未知等于已知,在内部是梯度变化最小。梯度在二阶偏导为0的时候取极值)
上f*的最简单的插值函数f:最小化问题的插值(在边界是未知等于已知,在内部是梯度变化最小。梯度在二阶偏导为0的时候取极值)
 (1)
(1)
其中
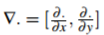 是梯度运算。最小值必须满足相关的拉格朗日方程。
是梯度运算。最小值必须满足相关的拉格朗日方程。
 (2)
(2)
其中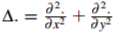 是拉普拉斯算子。
是拉普拉斯算子。
一个引导域是最小化问题(1)的扩展版本中使用的向量域v:(注意 v 是引导向量,也就是前景)
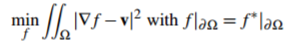 (3)
(3)
它的解是Dirichlet边界条件下泊松方程的唯一解:
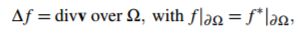 (4)
(4)
其中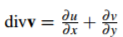 是v= (u,v)的散度。
是v= (u,v)的散度。
一个有用的替代方案是理解泊松插值所做的是定义 上修正的
上修正的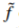 函数,以保证
函数,以保证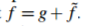 。
。
泊松方程(4)随之成为了以下有边界条件的拉普拉斯方程:
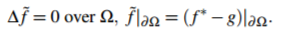 (5)
(5)
因此,在 内,我们添加的修正
内,我们添加的修正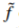 是就是边界
是就是边界 上源和目标错误匹配(f*-g)的一个插值(membrance interpolant)。这一引导插值的特例被用于无缝克隆。
上源和目标错误匹配(f*-g)的一个插值(membrance interpolant)。这一引导插值的特例被用于无缝克隆。
1-D EXAMPLE 一维的例子,这个可以自己上手计算跟着看,效果非常好
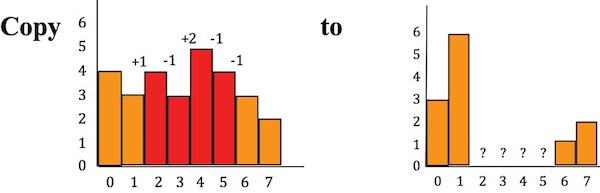
左边是原图,相当于前景,红色直方图就是引导向量。右边是背景图。想把左边红色部分移过去,但是又要变化最小,怎么办?那么就是计算
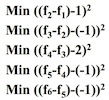 With f1 = 6, f6 = 1.
With f1 = 6, f6 = 1.
因为这些都是正数,也就相当于计算:
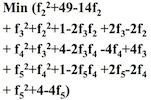
分开求偏导数
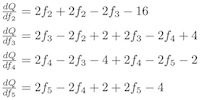
变化为矩阵
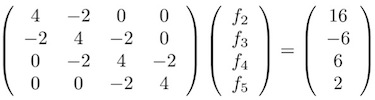
结论是:
f2 = 6, f3 = 4, f4 = 5, f5 = 3
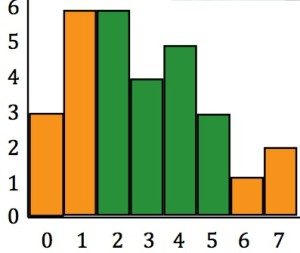
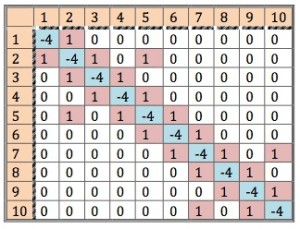
2-D EXAMPLE
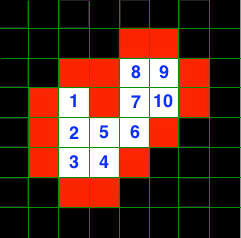
可以直接使用简化的方式,也就是拉普拉斯算子,进行卷积运算。

Poisson Blending(Seamless clone)研究和实现的更多相关文章
- 深度学习与计算机视觉(12)_tensorflow实现基于深度学习的图像补全
深度学习与计算机视觉(12)_tensorflow实现基于深度学习的图像补全 原文地址:Image Completion with Deep Learning in TensorFlow by Bra ...
- {ICIP2014}{收录论文列表}
This article come from HEREARS-L1: Learning Tuesday 10:30–12:30; Oral Session; Room: Leonard de Vinc ...
- 《Java学习笔记(第8版)》学习指导
<Java学习笔记(第8版)>学习指导 目录 图书简况 学习指导 第一章 Java平台概论 第二章 从JDK到IDE 第三章 基础语法 第四章 认识对象 第五章 对象封装 第六章 继承与多 ...
- android 自定义相机
老规矩,先上一下项目地址:GitHub:https://github.com/xiangzhihong/CameraDemo 方式: 调用Camera API 自定义相机 调用系统相机 由于需求不同, ...
- 图像融合之泊松融合(Possion Matting)
前面有介绍拉普拉斯融合,今天说下OpenCV泊松融合使用.顺便提一下,泊松是拉普拉斯的学生. 泊松融合的原理请参考这篇博文https://blog.csdn.net/u011534057/articl ...
- OpenCV实现"你的名字"滤镜
这是一个比较有意思的demo,用到了播送融合,具体效果见下图: 文件结构如图所示 主程序代码 #include"stdafx.h" #include<opencv2/phot ...
- cesium地下模式(地表透明)2
接上一篇博客,这篇直接分析火星的源码,看它到底改了些什么. 注意:在cesium1.63.1版本改变了模块化方式,由AMD改为ES6模块化.注意引入文件加载模块时做出对应修改. 1.火星代码里修改了4 ...
- js深入研究之扩展类,克隆对象,混合类(自定义的extend函数,clone函数,与augment函数)
1.类扩展 /* EditInPlaceField类 */ /* 扩展函数 */ function extend(subClass, superClass) { var F = function() ...
- 从点云到网格(三)Poisson重建
Possion重建是Kazhdan等2006年提出的网格重建方法[1].Possion重建的输入是点云及其法向量,输出是三维网格.Poisson有公开的源代码[2].PCL中也有Poisson的实现. ...
随机推荐
- 要学习的UML图
这是人人都是产品经理里的一节内容,这是个简单的例子,我觉得重要就摘抄一下 UML是要好好学习的一门课程呀
- 2018牛客网暑期ACM多校训练营(第二场) J - farm - [随机数哈希+二维树状数组]
题目链接:https://www.nowcoder.com/acm/contest/140/J 时间限制:C/C++ 4秒,其他语言8秒 空间限制:C/C++ 262144K,其他语言524288K ...
- POJ 1417 - True Liars - [带权并查集+DP]
题目链接:http://poj.org/problem?id=1417 Time Limit: 1000MS Memory Limit: 10000K Description After having ...
- POJ 1269 - Intersecting Lines - [平面几何模板题]
题目链接:http://poj.org/problem?id=1269 Time Limit: 1000MS Memory Limit: 10000K Description We all know ...
- POJ - 1054 The Troublesome Frog 模拟 枚举优化。
题意:有个R*C的格网.上面有若干个点,这些点可以连成一些直线,满足:这些点在直线上均匀排布(也就是间隔相等),直线的两段穿过网格(也就是第一个,最后一个在网格的边界附近) 求某条直线上最多的点数 题 ...
- cross browse compatible
不过我之前用过一个Chrome的插件叫浏览器兼容性检测工具,可以在内网测试,会自动监测网页的设计是否满足对应浏览器及版本的规范,不满足的话就会详细提示出来,不过有些过于专业性了,更适合开发人员查看,测 ...
- .windows安装使用这些偏底层的Python扩展太
.windows安装使用这些偏底层的Python扩展太不爽了,怎么彻底解决 error: Unable to find vcvarsall.bat呢? 1.不要按网上说的,安装MinGW,然后在“.. ...
- C++三大特性之继承
原文地址:https://qunxinghu.github.io/2016/09/12/C++%20%E4%B8%89%E5%A4%A7%E7%89%B9%E6%80%A7%E4%B9%8B%E7%B ...
- hbuilder和sublime的autoprefixer安装或者里sass的$mixin处理浏览器前缀
Autoprefixer是一个后处理程序,不象Sass以及Stylus之类的预处理器.它适用于普通的CSS,可以实现css3代码自动补全.也可以轻松跟Sass,LESS及Stylus集成,在CSS编译 ...
- 【Python】xpath中为什么粘贴进去代码后老报错?如何在定位元素的时候准确找到定位切入点?
1. xpath后()中双引号("")里面不能套用双引号(""),把里面的双引号改成单引号('')报错就没有了. 2.如何在定位元素的时候准确找到定位切入点? ...