Codeforces 15E Triangles - 组合数学

Last summer Peter was at his granny's in the country, when a wolf attacked sheep in the nearby forest. Now he fears to walk through the forest, to walk round the forest, even to get out of the house. He explains this not by the fear of the wolf, but by a strange, in his opinion, pattern of the forest that has n levels, where n is an even number.

In the local council you were given an area map, where the granny's house is marked by point H, parts of dense forest are marked grey (see the picture to understand better).

After a long time at home Peter decided to yield to his granny's persuasions and step out for a breath of fresh air. Being prudent, Peter plans the route beforehand. The route, that Peter considers the most suitable, has the following characteristics:

• it starts and ends in the same place — the granny's house;
• the route goes along the forest paths only (these are the segments marked black in the picture);
• the route has positive length (to step out for a breath of fresh air Peter has to cover some distance anyway);
• the route cannot cross itself;
• there shouldn't be any part of dense forest within the part marked out by this route;

You should find the amount of such suitable oriented routes modulo 1000000009.

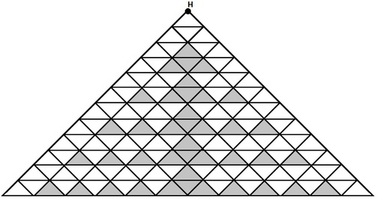
The example of the area map for n = 12 is given in the picture. Since the map has a regular structure, you can construct it for other n by analogy using the example.

Input

The input data contain the only even integer n (2 ≤ n ≤ 106).

Output

Output the only number — the amount of Peter's routes modulo 1000000009.

Examples

input

2

output

10

input

4

output

74

---

题目大意

　　首先，请仔细看图，找出图中的规律。

　　给定这个图的大小$n$，问有多少条有向路径满足：

• 路径长度为正
• 路径是沿着图中的边走的
• 路径不能自交
• 路径从H点开始，在H点结束
• 路径不能将黑色的格子圈住

　　答案模$10^{9}+9$。不是1e9 + 7。表示因为模数打错一发wa

　　　通过手动画图，可以发现，路径主要有2种

• 
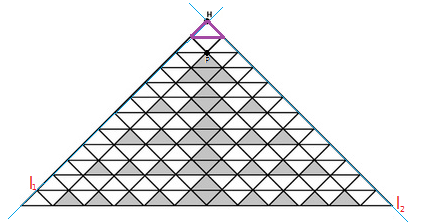
  这样的有向路径总共只有2条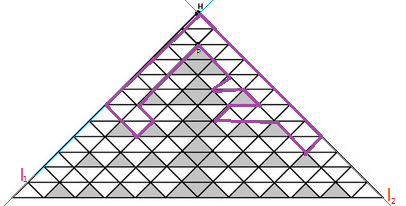
• 

  这样可以说是先在一侧乱窜，然后到点P，然后再到另一侧，最后在边上回到点H。

　　由于图是对称的，统计的是有向路径，所以只需要通过计算在一侧，点H到点P的合法的无向路径的数量然后再进行简单的运算就能够算出答案。

　　通过观察，可以发现，一旦从$l_{1}$上离开，就在到P点前不可能再回到$l_{1}$上。同时它也不可能继续向下走。

　　所以考虑从$l_{1}$上的某一点，向右或者向右下走一步然后到达点P 的方案数。

　　离开$l_{1}$后，就会沿大致向上的方向走，那么考虑在某个位置走到它的右上的方案数。

　　这个稍微分类讨论一下

1. 

   如果在这种地方，如果可以向右上走1步，那么方案数为1，否则为0。

2. 

   如果跑到了这里，设下凸的个数为$n$，它的方案数为$g_{n}$。（注意，以下讨论的方案数是指在保证路径合法的情况下）那么考虑点A到点C的方案数，显然为2。
   然后考虑点C到点B的方案数和点D到点B的方案数，显然它们是1，至于点C到点D呢，根据定义可得它是$g_{n - 1}$。
   然后想想，点A到点B的路径有哪几种？

   $A\rightarrow B,A\rightarrow C\rightarrow B, A\rightarrow C \rightarrow D \rightarrow B$

   于是不难根据加法原理得到

   $g_{n} = 2g_{n - 1} + 3$

　　然而有什么用呢？考虑刚离开$l_{1}$后到达的第一个点，那么它到点P的方案数就可以通过乘法原理计算。

　　紧接着就可以计算出在离开$l_{1}$上每个点后到达点P的方案数。然后把它们加起来就能够得到总的方案数，

　　假如成功算出了这样的总方案数为$s$，那么如何根据它来求答案呢？

　　容易根据加法和乘法原理得到：

$ans = 2s^{2} + 2$

　　说的很长，其实代码很短

Code

 /**
  * Codeforces
  * Problem#15E
  * Accepted
  * Time: 60ms
  * Memory: 2024k
  */
 #include <bits/stdc++.h>
 using namespace std;

 const int M = 1e9 + ;

 int n;

 inline void init() {
     scanf("%d", &n);
 }

 int sum = ;
 inline void solve() {
     for (int i = , last = -, P = ; i <= n; i++) {
         if (i & ) {
             last = ( * last + ) % M;
             P = (P * 1ll * last) % M;
         }
         sum = (sum + P) % M;
     }
     sum = (sum << ) % M;
     sum = (sum * 1ll * sum) % M;
     sum = ((sum + ) << ) % M;
     printf("%d", sum);
 }

 int main() {
     init();
     solve();
     return ;
 }