P1080国王游戏

传送

最大值最小什么的一看就是二分了qwq

然鹅并不知道怎么检查，所以我们换个思路

我们要求出最小的最大值，这肯定和大臣的排列有关，会不会有什么规律？

先看看只有两个大臣的情况

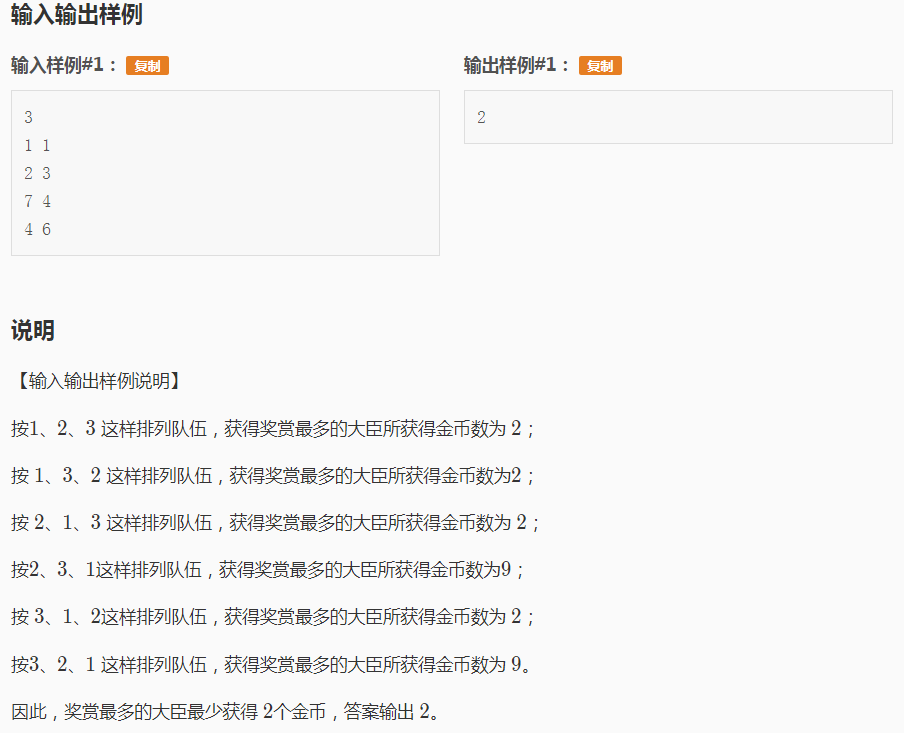
排列：1 2，ans1=max{a₀/b₁,a₀a₁/b₂}

排列：2 1，ans2=max{a₀/b₂,a₀a₂/b₁}

显然a₀/b₁<a₀a₂/b₁,a₀/b₂<a₀a₁/b₂,所以最大值取决于a₀a₁/b₂和a₀a₂/b₁

为了让最大值最小，当ans1>ans2的时候，我们就会调换1，2的顺序

所以就是a₀a₁/b₂>a₀a₂/b₁,也就是a₁b₁>a₂b₂的时候就会调换。

综上可得按照a*b从小到大排序

其实这个题的难点不在排序思路，在于高精。

a,b<10000,n<1000,最坏情况ans=10000¹⁰⁰⁰,爽

建议结合代码食用

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll read()
{
    char ch=getchar();
    ll x=;bool f=;
    while(ch<''||ch>'')
    {
        if(ch=='-')f=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return f?-x:x;
}
struct rr
{
    ll a,b;
}ren[];
ll n,aa,bb,sa[],now[],ma[],lenm=,lens=,lenn=;//sa记录大臣们左手上的数的乘积，now记录当前大臣的金币，ma记录最大值
bool cmp(rr t,rr w)
{
    return t.a*t.b<w.a*w.b;
}
//以下是高精
void cheng(ll k)//高精乘
{
    sa[]*=k;
    for(int i=;i<=lens;i++)
    {
        sa[i]=sa[i-]/+sa[i]*k;
        sa[i-]%=;
    }
    while(sa[lens]>=)
    {
        lens++;
        sa[lens]=sa[lens-]/;
        sa[lens-]%=;
    }
}
void chu(ll k)
{
    int j=,x=;
    memset(now,,sizeof(now));
    for(int i=lens;i>=;i--)
    {
        j++;
        x=x*+sa[i];
        now[j]=x/k;
        x=x-now[j]*k;
    }
    for(int i=;i<=j/;i++)//由于高精除单精是从第一位表示高位，所以要把now反过来，注意是i<=j/2,不是i<=j
      {
          int tmp=now[i];
          now[i]=now[j-i+];
          now[j-i+]=tmp;
      }
    while(now[j]==&&j>)
      j--;
    lenn=j;
}
void max_()//进行比较
{
    if(lenn>lenm)
    {
        for(int i=lenn;i>=;i--)
         ma[i]=now[i];
         lenm=lenn;//别漏了
        return ;
    }
    if(lenn<lenm) return ;
    for(int i=lenn;i>=;i--)
    {
        if(now[i]<ma[i])
         break;
        if(now[i]>ma[i])//找到第一位比ma对应位小的
        {
            for(int j=i;j>=;j--)
            {
                ma[j]=now[j];
            }
            return ;
        }
    }
    return ;
}
int main()
{
    sa[]=;
    n=read();ren[].a=read();ren[].b=read();
    for(int i=;i<=n;i++)
     ren[i].a=read(),ren[i].b=read();
    sort(ren+,ren++n,cmp);
    for(int i=;i<=n;i++)
    {
       cheng(ren[i-].a);
        chu(ren[i].b);
        max_();
    }
    for(int i=lenm;i>=;i--)
      printf("%lld",ma[i]);
}