HDU 2243 考研路茫茫——单词情结 ( Trie图 && DP && 矩阵构造幂和 )

题意 :  长度不超过L，只由小写字母组成的，至少包含一个词根的单词，一共可能有多少个呢？这里就不考虑单词是否有实际意义。

比如一共有2个词根 aa 和 ab ，则可能存在104个长度不超过3的单词，分别为
(2个) aa,ab, 
(26个)aaa,aab,aac...aaz, 
(26个)aba,abb,abc...abz, 
(25个)baa,caa,daa...zaa, 
(25个)bab,cab,dab...zab。

分析 : 这题和 POJ 2778 非常相似，如果没有做过 POJ 2778 建议先去搞定那道题。此题难点就在于这个是要求不超过 L 长度包含词根的单词，根据解决 POJ 2778 的经验，我们可以得出  答案 = 总单词种类数 - 不包含词根的单词数。首先总单词数可以很容易想到为 26¹ + 26² + 26³ + ..... + 26^L ，而不包含词根的单词总数可以这样得到 ==> 假设原 Trie 图构建出来的状态矩阵为 A ，那么同样的我们需要构造一个幂和即 A¹ + A² + A³ + ..... + A^L 然后最后的答案便是 ∑A^L(0, i)  ( i ∈ 1~矩阵长度 ) ，那怎么去构造这两个幂和呢？

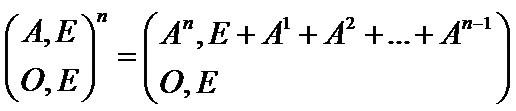
只要利用这个公式即可，用原矩阵 + 单位矩阵 + 零矩阵构造出新矩阵，最后右上角的矩阵便是幂和的矩阵！

这里还有一点要注意，就是对于 2^64次方求模有一个很巧的方法，也就是直接定义为 unsigned long long （范围 : 0 ~ 2^64 -1），溢出就相当于求模了！

#include<string.h>
#include<stdio.h>
#include<iostream>
#include<queue>
#define ULL unsigned long long
using namespace std;

;
;
int maxn;///矩阵的大小
];

][]; }unit, M;
mat operator * (mat a, mat b){
    mat ret;
    ; i<maxn; i++){
        ; j<maxn; j++){
            ret.m[i][j] = (ULL);
            ; k<maxn; k++){
                ret.m[i][j] += a.m[i][k]*b.m[k][j];
            }
        }
    }
    return ret;
}

inline void init_unit() {
    ; i<maxn; i++)
        unit.m[i][i] = ;
}

mat pow_mat(mat a, long long n){
    mat ret = unit;
    while(n){
        ) ret = ret * a;
        a = a*a;
        n >>= ;
    }
    return ret;
}

struct Aho{
    struct StateTable{
        int Next[Letter];
        int fail, flag;
    }Node[Max_Tot];
    int Size;
    queue<int> que;

    inline void init(){
        while(!que.empty()) que.pop();
        memset(Node[].Next, , ].Next));
        Node[].fail = Node[].flag = ;
        Size = ;
    }

    inline void insert(char *s){
        ;
        ; s[i]; i++){
            int idx = s[i] - 'a';
            if(!Node[now].Next[idx]){
                memset(Node[Size].Next, , sizeof(Node[Size].Next));
                Node[Size].fail = Node[Size].flag = ;
                Node[now].Next[idx] = Size++;
            }
            now = Node[now].Next[idx];
        }
        Node[now].flag = ;
    }

    inline void BuildFail(){
        Node[].fail = -;
        ; i<Letter; i++){
            ].Next[i]){
                Node[Node[].Next[i]].fail = ;
                que.push(Node[].Next[i]);
            }].Next[i] = ;///必定指向根节点
        }
        while(!que.empty()){
            int top = que.front(); que.pop();
            ;
            ; i<Letter; i++){
                int &v = Node[top].Next[i];
                if(v){
                    que.push(v);
                    Node[v].fail = Node[Node[top].fail].Next[i];
                }else v = Node[Node[top].fail].Next[i];
            }
        }
    }

    inline void BuildMatrix(){
        ; i<Size; i++)
            ; j<Size; j++)
                M.m[i][j] = ;
        ; i<Size; i++){
            ; j<Letter; j++){
                if(!Node[i].flag && !Node[ Node[i].Next[j] ].flag)
                    M.m[i][Node[i].Next[j]]++;
            }
        }
        maxn = Size;
    }
}ac;

ULL GetSum(long long num){
    mat ret;
    ret.m[][] = ;
    ret.m[][] = ;
    ret.m[][] = ;
    ret.m[][] = ;
    int tmp = maxn;
    maxn = ;
    ret = pow_mat(ret, ++num);
    maxn = tmp;
    ][]-;
}

ULL GetElimination(long long num){
    mat tmp;
    ; i<maxn; i++)///左上角 为 原矩阵
        ; j<maxn; j++)
            tmp.m[i][j] = M.m[i][j];

    ; i<maxn; i++)///右上角 为 单位矩阵
        ); j++)
            tmp.m[i][j] = (i+maxn == j);

    ); i++)///左下角 为 零矩阵
        ; j<maxn; j++)
            tmp.m[i][j] = ;

    ); i++)///右下角 为 单位矩阵
        ); j++)
            tmp.m[i][j] = (i==j);

    int Temp = maxn;
    maxn <<= ;///先将原本矩阵的大小放大一倍进行快速幂运算，这个和我快速幂的写法有关
    tmp = pow_mat(tmp, ++num);
    ULL ret = (ULL);
    maxn = Temp;///再回复成原来大小
    ); i++)///右上角的矩阵就是幂和了
        ret += tmp.m[][i];

    return (--ret);///需要 -1
}

int main(void)
{
    int n, m;

    while(~scanf("%d %d", &m, &n)){
        ac.init();
        ; i<m; i++){
            scanf("%s", S);
            ac.insert(S);
        }
        ac.BuildFail();
        ac.BuildMatrix();
        init_unit();
        ULL Tot = GetSum((long long)n);///注意是传long long不然会爆int
        ULL Elimination = GetElimination((long long)n);
        cout<<Tot-Elimination<<endl;
    }
    ;
}