线性回归，附tensorflow实现

本文同步自：https://zhuanlan.zhihu.com/p/30738405

本文旨在通过介绍线性回归来引出一些基本概念：h(x)，J(θ)，梯度下降法

有一组数据：

x=[1,2,3,4,5,6,7,8,9,10]

y=[1,2,3,4,5,6,7,8,9,10]

要求画一条过原点的直线，穿过上述所有点

这组数据在二维平面表现如下

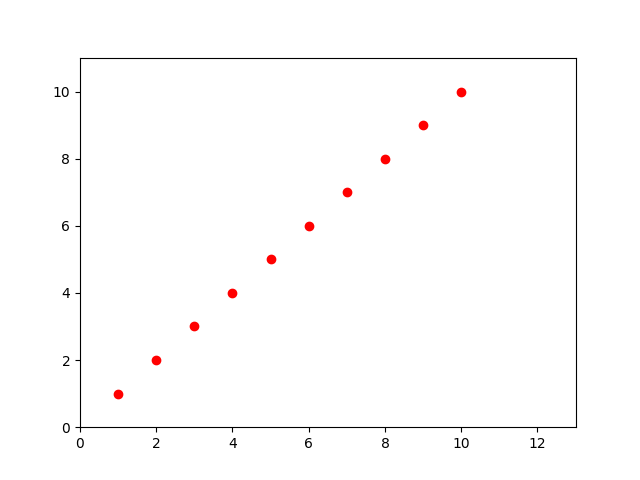
引入概念，假设函数：h(x)。h代表hypothesis

由于是过原点的直线，所以可以列出方程h(x)：

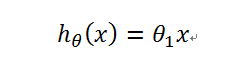
先随意假设一个 ，在这先假设 =0.5 ，函数图如下

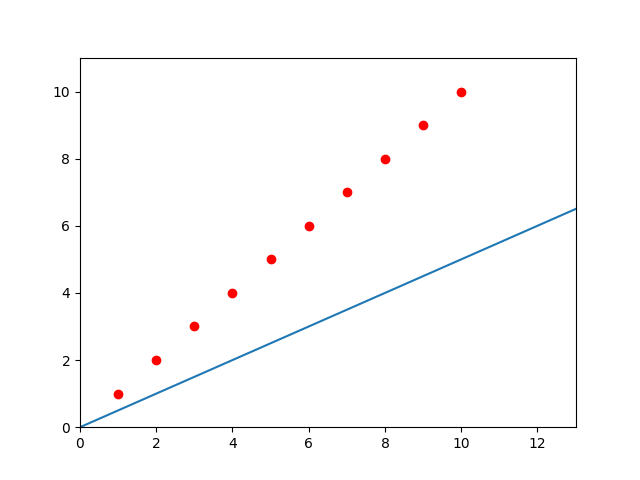
显而易见这条直线并不是我们想要的。那么具体的，怎么判断一条直线的好坏呢

引入概念代价函数 cost function

在本例中，可以由拟合数据和原始数据对应点的误差的平方的均值来判断直线的好坏；列出J(θ)如下：

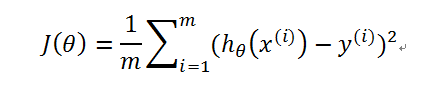
其中m表示数据的总量，在本题中为10； 并不是代表x的i次方，而是代表第i个x的数值，例如在本例中， 为2

将h(x)带入，得

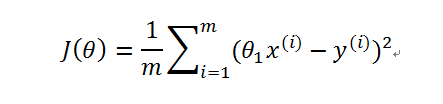
函数图是这样一个形状，数值对不上，凑合着看吧；有一点值得注意，在J(θ)中， 与 都应该作为常量来处理

显然，J(θ)值越小，点到直线的距离总和越少，画出来的直线效果也就越好。放到题目中就是当J(θ)=0的时候，画出的直线穿过了所有的点

那么问题就变成了如何最小化J(θ)

在这个例子中可以手动计算，也就是正规方程法，但是随着问题复杂度的增加，正规方程法的实用性会越来越低

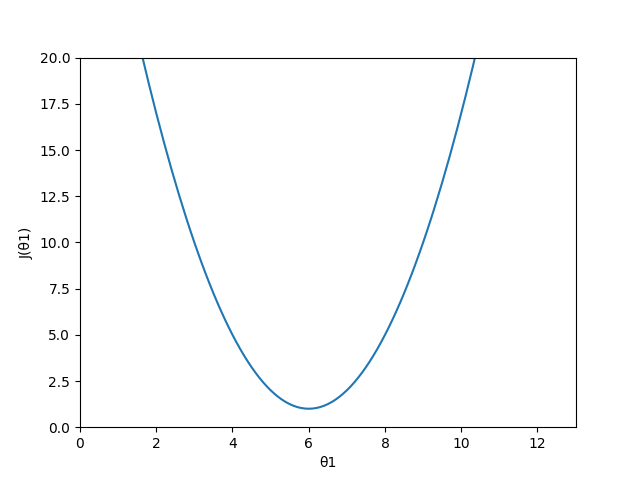
引入梯度下降法

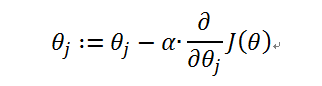
其中α为步幅

梯度下降法可以解释为：对J(θ)求关于 （本例中只有 ）的偏导数并乘以步幅，再用 减去该值，得到的结果赋值给 。此过程需要重复多次

步幅的选择会直接关系到梯度下降法的效果，如下图

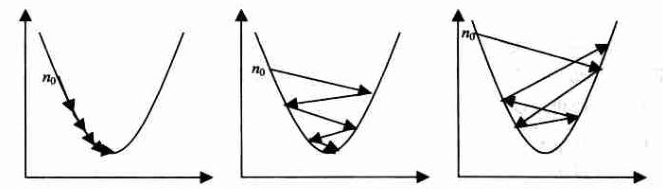
当选取了一个较小步幅的时候，将正确收敛

当选取了一个较大步幅的时候，将震荡收敛

当选取了一个过大步幅的时候，将无法收敛

调整一下例子

x=[5,6,7,8,9,10,11,12,13,14]

y=[1,2,3,4,5,6,7,8,9,10]

要求画一条直线，穿过上述所有点

很明显，对于这组数据，仅仅是过原点的直线无法满足要求，所以列出新的h(x)：

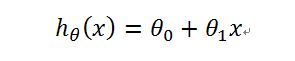
而判断一条直线的好坏还可以沿用之前的J(θ)：

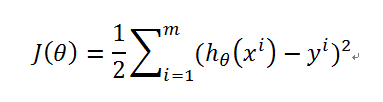
函数图是这样一个形状，数值对不上，凑合着看吧

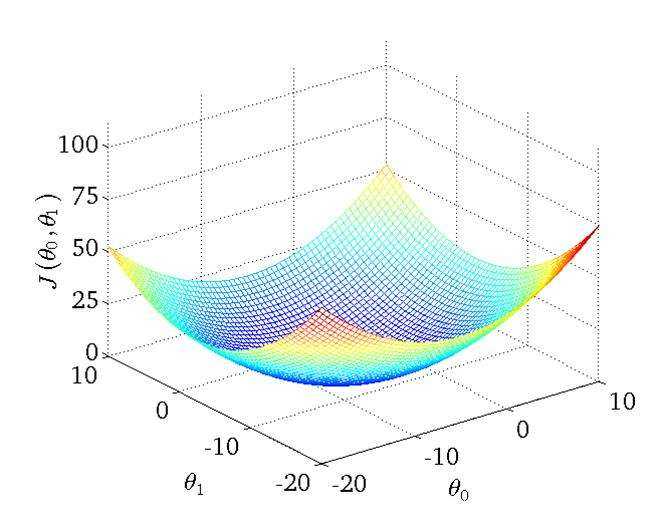
之后就是如何最小化J(θ)的问题了。下面给出tensorflow的代码实现

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# Parameters
learning_rate = 0.05
training_epochs = 2000
display_step = 50
# Training Data
train_X = np.asarray([5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0, 13.0, 14.0])
train_Y = train_X - 4
paint_X = np.asarray([-100.0, 100.0])

n_samples = train_X.shape[0]
# tf Graph Input
X = tf.placeholder("float")
Y = tf.placeholder("float")

# Set model weights
W = tf.Variable(-10., name="weight")
b = tf.Variable(10., name="bias")
# Construct a linear model
pred = tf.add(tf.multiply(X, W), b)
# Mean squared error
cost = tf.reduce_sum(tf.pow(pred - Y, 2)) / (2 * n_samples)
# Gradient descent
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
# Initializing the variables
init = tf.global_variables_initializer()
# Launch the graph

plt.figure()
plt.ion()

with tf.Session() as sess:
    sess.run(init)

    # Fit all training data
    for epoch in range(training_epochs):
        for (x, y) in zip(train_X, train_Y):
            sess.run(optimizer, feed_dict={X: x, Y: y})

        # Display logs per epoch step
        if (epoch + 1) % display_step == 0:
            c = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
            print("Epoch:", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(c),
                  "W=", sess.run(W), "b=", sess.run(b))

            plt.axis([0.0, np.max(train_X) + 1, 0.0, np.max(train_Y) + 1])
            plt.plot(train_X, train_Y, 'ro', label='Original data')
            plt.plot(paint_X, sess.run(W) * paint_X + sess.run(b), label='Fitted line')
            plt.pause(0.001)
            plt.clf()

    print("Optimization Finished!")
    training_cost = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
    print("Training cost=", training_cost, "W=", sess.run(W), "b=", sess.run(b), '\n')

    plt.axis([0.0, np.max(train_X) + 1, 0.0, np.max(train_Y) + 1])
    plt.plot(train_X, train_Y, 'ro', label='Original data')
    plt.plot(paint_X, sess.run(W) * paint_X + sess.run(b), label='Fitted line')
    plt.pause(10)